SOLVING WORD PROBLEMS WITH CUBOID

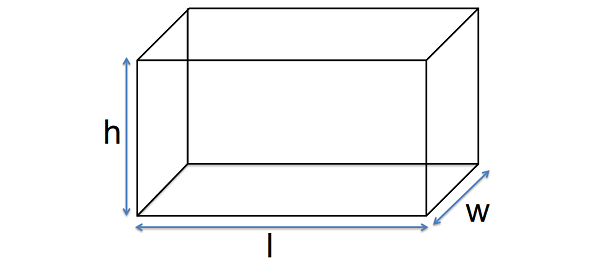
Formulas given below can be used to find volume, lateral surface area and total surface of a cuboid.   

Volume = l x w x h cubic units

Lateral surface area = 2h(l + w) square units

Total surface area = 2(lw + wh + hl) squareunits

Problem 1 :

Find the total surface area and lateral surface area of a cuboid whose length is 20 cm, width is 15 cm and height is 8 cm.

Solution :

Total surface area :

= 2(lw + wh + hl)

Substitute.

= 2[20(15) + 15(8) + 8(20)]

= 2 [300 + 120 + 160]

= 2(580)

= 1160 cm²

Lateral surface area :

= 2h(l + w)

Substitute.

= 2(8)(20 + 15)

= 16(35)

= 560 cm²

Problem 2 :

The dimensions of a cuboidal box are 6 m x 400 cm x 1.5 m. Find the cost of painting its entire outer surface at the rate of $22 per square meter.

Solution :

From the given information,

length (l) = 6 m

width (w) = 400 cm = 400/100 m = 4 m

height = 1.5 m

Outer surface area has six sides.

Then, the required area is

= 2(lw + wh + hl)

Substitute.

= 2[6(4) + 4(1.5) + 1.5(6)]

= 2[24 + 6 + 9]

= 2[39]

= 78 m²

Cost of painting the surface is $22 per m².

So, the required cost is

= 78(22)

 = $1716

Problem 3 :

The dimensions of a hall is 10 m x 9 m x 8 m. Find the cost of white washing the walls and ceiling at the rate of $8.50 per square meter. 

Solution :

From the given information,

length (l) = 10 m

width (w) = 9 m

height = 8 m

Area of white washing is

= 2h(l + w) + lw

Substitute. 

= 2(8)(10 + 9) + 10(9)

= 16(19) + 90

 = 304 + 90

  = 394 m²

Cost of white washing is $8.50 per m².

So, the required cost is

= 394(8.50)

= $3349

Problem 4 :

The length, width and depth of a pond are 20.5 m, 16 m and 8 m respectively. Find the capacity of the pond in liters.

Solution :

l = 20.5 m, w = 16 m, h = 8 m

Capacity of pond : 

= lx w x h

= 20.5(16)(8)

= 2624 m³

1 m³ = 1000 liters, 

= 2624(1000) liters

= 2624000 liters

Problem 5 :

The outsides of purple traps are coated with glue to catch emerald ash borers. You make your own trap in the shape of a rectangular prism with an open top and bottom. What is the surface area that you need to coat with glue?

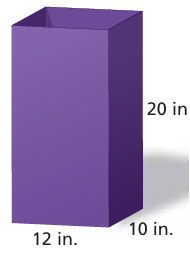
Solution :

Faces to be covered with glue are front, back, side faces

Length = 12 inches

Width = 10 inches

Height = 20 inches

Lateral surface area = 2lh + 2wh

= 2h(l + w)

= 2(20)(12 + 10)

= 40 (22)

= 880 square inches

Problem 6 :

Which prism has the greater surface area?

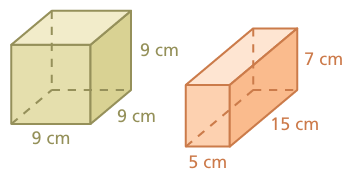
Solution :

Total surface area of rectangular prism = 2(lw + wh + hl)

Total surface area of cube = 6a²

Side length of cube = 9 cm

length = 15 cm, width = 5 cm and height = 7 cm

= 2[15(5) + 5(7) + 7(15)]

= 2[75 + 35 + 105]

= 2(215)

= 430 cm square.

Surcea area of cube = 6(9)²

= 6(81)

= 486 cm square

Problem 7 :

A public library has an aquarium in the shape of a rectangular prism. The base is 6 feet by 2.5 feet. The height is 4 feet. How many square feet of glass were used to build the aquarium? (The top of the aquarium is open.)

Solution :

To create a aquarium, we need to cover five faces.

Area of front and back + area of side faces + area of bottom

= 2(length x height) + 2(width x height) + length x width

length = 6 feet, width = 2.5 feet and height = 4 feet

= 2(6 x 4) + 2(2.5 x 4) + (4 x 2.5)

= 2(24) + 2(1) + 10

= 48 + 2 + 10

= 60 sqaure feet

So, to make a aquarium, we need 60 square feet of glass.

Problem 8 :

A label that wraps around a box of golf balls covers 75% of its lateral surface area. What is the value of x?

Solution :

Measures of lable :

length = 3 inches, width = 2 inches and height = 2 inches

Measures of box :

Length = x, width = 2 inches and height = 2 inches

Lateral surface area = 2

Surface area = 2 lh + 2lw

= 2l(h + w)

Surface area covered by lable = 75% of surface area covered by box

2(3)(2 + 2) = 75% of 2(x)(2 + 2)

6(4) = 0.75(2x)(4)

6 = 1.5x

x = 6/1.5

x = 4 feet

So, the required length of the box is 4 feet.

Problem 9 :

Write a formula for the surface area of a rectangular prism using the height h, the perimeter P of a base, and the area B of a base.

Solution :

Height of the rectangular prism = h

Perimeter of the base = P

Area of the base = B

Total surface area of rectangular prism = 2(lw + w h + hl)

= 2lw + 2w h + 2hl

Area of base of top and bottom = 2 l w ==> 2 B

2wh + 2hl = 2h(w + l)

= 2(w + l) h

= hP

Replacing the above values in the formula, we get

total surface area of rectangular prism = 2B + Ph

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.