SOLVING PAIR OF LINEAR EQUATIONS USING ELIMINATION METHOD WORKSHEET

Example 1 :

2x + 3y = 5

x - 3y = -2

Solution

Example 2 :

3x - 2y = 1

5x - 3y = 3

Solution

Example 3 :

1/2x + 1/3y = 2

1/3x + 1/2y = 13/6

Solution

Example 4 :

2/√x + 3/√y = 2

4/√x – 9/√y = -1

Solution

Example 5 :

4/x + 3y = 14

3/x – 4y = 23

Solution

Question 1 :

Solve the pair of linear equations using elimination method.

10/(x + y) + 2/(x –y)  =  4 and 15/(x + y) – 5/(x – y)  =  -2

Solution

Question 2 :

Solve the pair of linear equations using elimination method.

1/(3x + y) + 1/(3x – y)  =  3/4

and

 1/2(3x + y) - 1/2(3x – y)  =  -1/8

Solution

Question 3 :

In a football game, all of the home team’s points are from 7-point touchdowns and 3-point field goals. The team scores six times. Write and solve a system of linear equations to find the numbers of touchdowns and field goals that the home team scores.

Solution

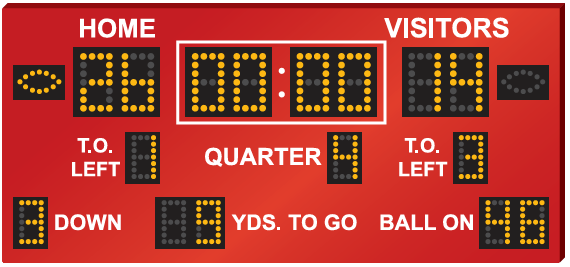
Question 4 :

You are an ecologist studying the populations of two types of fish in a lake. Use the information in the table to predict when the populations of the two types of fish will be equal.

Solution

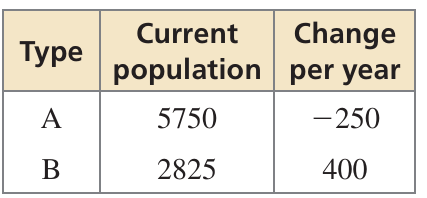
Question 5 :

Your family needs to rent a car for a week while on vacation.

• Company A charges $3.25 per mile plus a flat fee of $125 per week.
• Company B charges $3 per mile plus a flat fee of $150 per week.

After how many miles of travel are the total costs the same at both companies?

Solution

Question 6 :

You need to hire a catering company to serve meals to guests at a wedding reception. Company A charges $500 plus $20 per guest. Company B charges $800 plus $16 per guest. For how many guests are the total costs the same at both companies?

Solution

Problem 1 :

A fraction becomes 9/11, if 2 is added to both numerator and the denominator. If 3 be added to both the numerator and the denominator, the fraction becomes 5/6. Find the fraction.

Solution

Problem 2 :

Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?

Solution

Problem 3 :

The perimeter of the trapezoidal piece of land is 48 kilometers. The perimeter of the rectangular piece of land is 144 kilometers. Write and solve a system of linear equations to fi nd the values of x and y.

Solution

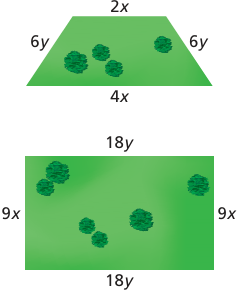
Problem 4 :

A small bag of trail mix contains 3 cups of dried fruit and 4 cups of almonds. A large bag contains 4 1/2 cups of dried fruit and 6 cups of almonds. Write and solve a system of linear equations to find the price of 1 cup of dried fruit and 1 cup of almonds.

Solution

Problem 5 :

You plant a spruce tree that grows 4 inches per year and a hemlock tree that grows 6 inches per year. The initial heights are shown.

a. Write a system of linear equations that represents this situation.

b. Interpret your solution.

Solution

Problem 6 :

It takes you 3 hours to drive to a concert 135 miles away. You drive 55 miles per hour on highways and 40 miles per hour on the rest of the roads.

a. How much time do you spend driving at each speed?

b. How many miles do you drive on highways? the rest of the roads?

Solution

Problem 1 :

The coach of a cricket team buys 7 bats and 6 balls for $3800. Later, she buys 3 bats and 5 balls for $1750. Find the cost if each bat and each ball.

Solution

Problem 2 :

The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is $105 and for a journey of 15 km, the charge paid is $155. What are the fixed charge and charge per km ? How much does a person have to pay for traveling a distance of 25 km ?

Solution

Problem 3 :

The circle graph shows the results of a survey in which 50 students were asked about their favorite meal.

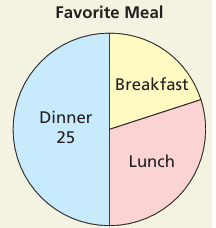
a. Estimate the numbers of students who chose breakfast and lunch.

b. The number of students who chose lunch was 5 more than the number of students who chose breakfast. Write a system of linear equations that represents the numbers of students who chose breakfast and lunch.

c. Explain how you can solve the linear system in part (b) to check your answers in part (a).

Solution

Problem 4 :

A rectangle has a perimeter of 18 inches. A new rectangle is formed by doubling the width w and tripling the lengthℓ, as shown. The new rectangle has a perimeter P of 46 inches.

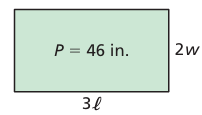
a. Write and solve a system of linear equations to find the length and width of the original rectangle.

b. Find the length and width of the new rectangle.

Solution

1)  the cost of each bat is $500 and each ball is $50.

2)  Therefore, the fixed charge is $5 and charge per km for the distance covered is $10.

3)  

• Number of students who choose lunch is 10
• Number of students who choose breakfast is 15.

4)  

3l ==> 3(10) ==> 30 inches

2w ==> 2(8) ==> 16 inches

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.