SOLVING SYSTEM OF LINEAR EQUATIONS WORD PROBLEMS IN 2 VARIABLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
A fraction becomes 9/11, if 2 is added to both numerator and the denominator. If 3 be added to both the numerator and the denominator, the fraction becomes 5/6. Find the fraction.
Solution :
Let x/y be the required fraction
If 2 is added to both numerator and denominator the fraction becomes 9/11.
(x + 2)/(y+2) = 9/11
11(x + 2) = 9(y + 2)
11x + 22 = 9y + 18
11x – 9y = 18 – 22
11x – 9y = -4 ------(1)
If 3 is added to both the numerator and the denominator it becomes 5/6.
(x + 3)/(y+3) = 5/6
6(x + 3) = 5(y + 3)
6x + 18 = 5y + 15
6x – 5y = 15 - 18
6x – 5y = - 3 ------(2)
Solving (1) and (2), we get
x = 7
Substitute 7 for x in (1).
(1)-----> 11(7) – 9y = -4
77 – 9y = -4
-9y = -81
y = 9
Then,
x/y = 7/9
So, the required fraction is 7/9.
Problem 2 :
Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?
Solution :
Let x be the age of Jacob and y be the age of his son.
5 years hence their ages will be
x + 5 and y + 5
x + 5 = 3(y + 5)
x + 5 = 3y + 15
x – 3y = -5 + 15
x – 3y = 10 ------(1)
5 years ago, their ages were
x – 5 and y – 5
x – 5 = 7(y – 5)
x – 5 = 7y – 35
x – 7y = 5 - 35
x – 7y = -30 ------(2)
(1) - (2) :
4y = 40
y = 10
Substitute 10 for y in (2).
(2)------> x - 7(10) = -30
x – 70 = -30
x = 40
Therefore,
age of Jacob's son = 10
Age of Jacob = 40
Problem 3 :
The perimeter of the trapezoidal piece of land is 48 kilometers. The perimeter of the rectangular piece of land is 144 kilometers. Write and solve a system of linear equations to fi nd the values of x and y.
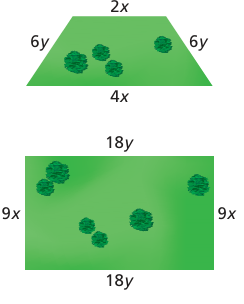
Solution :
Perimeter of trapezoid = 48 km
2x + 4x + 6y + 6y = 48
6x + 12y = 48
Dividing by 6, we get
x + 2y = 8 --------(1)
Perimeter of rectangle = 144 km
2 (18y + 9x) = 144
9x + 18y = 72
Dividing by 9, we get
x + 2y = 8 -------(2)
The the system of linear equations has infinitely many solutions.
Problem 4 :
A small bag of trail mix contains 3 cups of dried fruit and 4 cups of almonds. A large bag contains 4 1/2 cups of dried fruit and 6 cups of almonds. Write and solve a system of linear equations to find the price of 1 cup of dried fruit and 1 cup of almonds.

Solution :
Let x be the cost of 1 cup of dried fruit and y be the cost of 1 cup of almonds.
3x + 4y = 6 -------(1)
4.5x + 6y = 9 -------(2)
Multiplying the (1) by 3 and multiplying (2) by -2
9x + 12y + (-9x - 12y) = 18 + (-18)
9x - 9x + 12y - 12y = 18 - 18
So, the system has infinitely many solution.
Problem 5 :
You plant a spruce tree that grows 4 inches per year and a hemlock tree that grows 6 inches per year. The initial heights are shown.
a. Write a system of linear equations that represents this situation.
b. Interpret your solution.

Solution :
Let x be the number of years required to reach the same of height of both trees.
Let y be the same height reached by both trees.
|
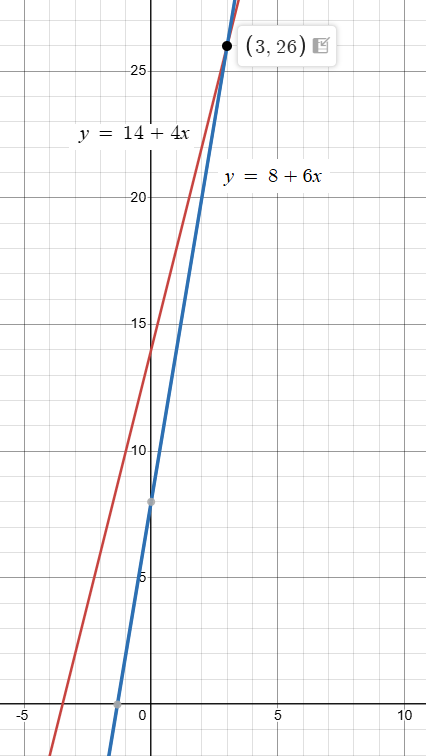
Spruce tree : y = 14 + 4x ----(1) |
Hemlock tree : y = 8 + 6x -----(2) |
(1) = (2)
14 + 4x = 8 + 6x
4x - 6x = 8 - 14
-2x = -6
x = 3
Applying x = 3, we get
y = 14 + 4(3)
y = 14 + 12
y = 26
After 3 years, both tree will get the height of 26 inches.
Problem 6 :
It takes you 3 hours to drive to a concert 135 miles away. You drive 55 miles per hour on highways and 40 miles per hour on the rest of the roads.
a. How much time do you spend driving at each speed?
b. How many miles do you drive on highways? the rest of the roads?
Solution :
Let x be the time spent on highways
Let y be the time spent on rest of the roads.
x + y = 3 -----(1)
55x + 40y = 135 -----(2)
From (1), y = 3 - x
55x + 40(3 - x) = 135
55x + 120 - 40x = 135
15x + 120 = 135
15x = 135 - 120
15x = 15
x = 15/15
x = 1
Applying x = 1, y = 3 - 1 ==> 2
So, 1 hour spent on highways and 2 hours spent on rest of the roads.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 14)
Dec 20, 25 09:54 AM
Digital SAT Math Problems and Solutions (Part - 14) -
US Common Core K-12 Curriculum Algebra Word Problems
Dec 20, 25 01:19 AM
US Common Core K-12 Curriculum Algebra Word Problems on Systems of LInear Equations -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Dec 20, 25 01:18 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations
