SUBSTITUTION METHOD WORD PROBLEMS AND ANSWERS

Problem 1 :

The coach of a cricket team buys 7 bats and 6 balls for $3800. Later, she buys 3 bats and 5 balls for $1750. Find the cost if each bat and each ball.

Solution :

Let "x" be the cost of each bat.

Let "y" be the cost of  each ball.

Then, 

7x + 6y  =  3800 -----(1)

3x + 5y  =  1750 -----(2)

Solve (1) for y.

6y  =  3800 - 7x

y  =  (3800 - 7x)/6 -----(3)

Substitute y  =  (3800 - 7 x)/6 in (2)

(2)-----> 3x + 5(3800 - 7x)/6  =  1750

 [18x + 5(3800 - 7x)]/6  =  1750

(18x + 19000 - 35x)/6  =  1750

-17x + 19000  =  1750(6)

-17x + 19000  =  10500

-17x  =  10500 - 19000

-17x  =  -8500

x  =  8500/17

x  =  500

Substitute x  =  500 in (3)

(3)-----> y  =  [3800 - 7(500)] / 6

y  =  (3800 - 3500) / 6

y  =  300/6

y  =  50

So, the cost of each bat is $500 and each ball is $50.

Problem 2 :

The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is $105 and for a journey of 15 km, the charge paid is $155. What are the fixed charge and charge per km ? How much does a person have to pay for traveling a distance of 25 km ?

Solution :

Let "x" be the fixed charge

Let "y" be the charge  per km for the distance covered

 x + 10y  =  105 ------(1)

 x + 15y  =  155 ------(2)

Solving (1) for x.

x  =  105 - 10y -----(3)

Substitute x  =  105 - 10y in (2).

(2)-----> 105 - 10y + 15y  =  155

105 + 5y  =  155

5y  =  50

y  =  10

Substitute y  =  10 (3).

(30-----> x  =  105 -10(10)

x  =  105 - 100

x  =  5

Therefore, the fixed charge is $5 and charge per km for the distance covered is $10.

Amount has to be paid for a travel of 25 km is 

=  5 + 25(10)

=  5 + 250

=  $255

Problem 3 :

The circle graph shows the results of a survey in which 50 students were asked about their favorite meal.

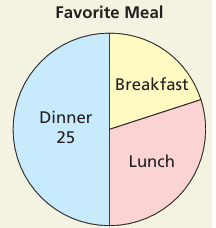
a. Estimate the numbers of students who chose breakfast and lunch.

b. The number of students who chose lunch was 5 more than the number of students who chose breakfast. Write a system of linear equations that represents the numbers of students who chose breakfast and lunch.

c. Explain how you can solve the linear system in part (b) to check your answers in part (a).

Solution :

Let x be the number of students who choose lunch.

Let y be the number of students who choose breakfast.

y = x + 5 ------(1)

Number of students who choose dinner, breakfast and lunch = 50

25 + x + y = 50

x + y = 50 - 25

x + y = 25 --------(2)

Applying the value of y in (1), we get

x + x + 5 = 25

2x + 5 = 25

2x = 25 - 5

2x = 20

x = 20/2

x = 10

When x = 10, y = 10 + 5

y = 15

• Number of students who choose lunch is 10
• Number of students who choose breakfast is 15.

Problem 4 :

A rectangle has a perimeter of 18 inches. A new rectangle is formed by doubling the width w and tripling the lengthℓ, as shown. The new rectangle has a perimeter P of 46 inches.

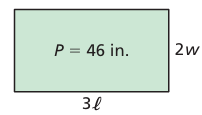
a. Write and solve a system of linear equations to find the length and width of the original rectangle.

b. Find the length and width of the new rectangle.

Solution :

Perimeter of rectangle = 18 inches

Perimeter of new rectangle = 46 inches

Let l and w be the length and width of old rectangles respectively.

l + w = 18 --------(1)

3l + 2w = 46 --------(2)

From (1)

w = 18 - l

Applying the value of w in (2), we get

3l + 2(18 - l) = 46

3l + 36 - 2l = 46

l = 46 - 36

l = 10 inches

w = 18 - 10

w = 8 inches

3l ==> 3(10) ==> 30 inches

2w ==> 2(8) ==> 16 inches

Problem 5 :

The perimeter of the trapezoidal piece of land is 48 kilometers. The perimeter of the rectangular piece of land is 144 kilometers. Write and solve a system of linear equations to find the values of x and y.

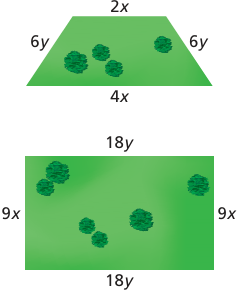
Solution :

Perimeter of trapezoid = 48 km

2x + 4x + 6y + 6y = 48

6x + 12y = 48

Dividing by 6, we get

x + 2y = 8 --------(1)

Perimeter of rectangle = 144 km

2 (18y + 9x) = 144

9x + 18y = 72

Dividing by 9, we get

x + 2y = 8 -------(2)

The the system of linear equations has infinitely many solutions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.