SPECIFYING UNITS OF MEASURE

Core Concept : Operations and Unit Analysis

Addition and Subtraction :

When you add or subtract quantities, they must have the same units of measure. The sum or difference will have the same unit of measure.

For example, let us cosider two quantities 5 cm and 3 cm.

Let us find the sum and difference of the above two quantities.

5 cm + 3 cm = 8 cm

5 cm - 3 cm = 2 cm

When we find the sum and difference of two quantities with the same units (cm), the results also have the same units (cm).

Consider the rectangle shown below.

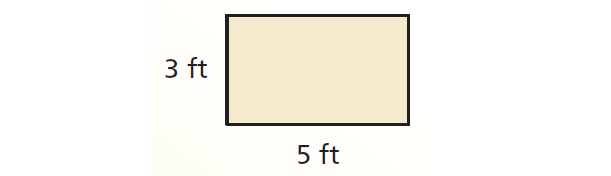
To get the perimeter of a rectangle, we have to add the lengths of all the sides. And also, opposite sides of a rectangle are equal in length.

Perimeter = (3 ft) + (5 ft) + (3 ft) + (5 ft)

= 16 feet

When you add feet, you get feet.

Multiplication and Division :

When we multiply or divide quantities, the product or quotient will have a different unit of measure.

For example, let us find the area of the rectangle shown above. 

Area of rectangle = length X width

= (3 ft) X (5 ft)

= 15 square feet

When we multiply feet by feet, we get feet squared or square feet.

Solved Problems

Problem 1 :

You work 8 hours and earn $72. What is your hourly wage?

Solution :

Hourly wage ($ per hour) = Total earnings ÷ no. of hours

= $72 ÷ 8 hours

= $9 per hour

(The units on each side of the equation balance. Both are
specified in dollars per hour.)

Your hourly wage is $9 per hour.

Problem 2 :

The length of each of a cube is 5 cm. What is the volume of the cube?

Solution :

Volume of the cube = (5 cm)(5 cm)(5 cm)

= 125 cubic cm.

Problem 3 :

The population of the United States was about 280 million in 2000 and about 310 million in 2010. What was the annual rate of change in population from 2000 to 2010?

Solution :

Annual rate of change in population from 2000 to 2010 :

= 3 million per year

Problem 4 :

You drive 240 miles and use 8 gallons of gasoline. What was your car’s gas mileage (in miles per gallon)?

Solution :

Car's gas mileage (in miles per gallon) :

= 30 miles per gallon

Problem 5 :

A bathtub is in the shape of a rectangular prism. Its dimensions are 5 feet by 3 feet by 18 inches. The bathtub is three-fourths full of water and drains at a rate of 1 cubic foot per minute. About how long does it take for all the water to drain?

Solution :

First, let us find the capacity of the bathtub using the given dimensions. Since bathtub is in the shape of rectangular prsim, we can use the formula ℓ X h X w (formula to find volume of a rectangular prsim) to find the capacity of the bathtub.

Capacity of bathtub : 

= (5 ft)((3 ft)( 18 in)

(12 in = 1 ft ----> 18 in = 1.5 ft) 

= (5 ft)((3 ft)( 1.5 ft)

= 22.5 cubic feet

Amount of water in bathtub :

= ¾(22.5 cubic feet)

= 16.875 cubic feet

Time taken for all the water (16.875 cubic feet) to drain :

= 16.875 minutes

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.