SOLVE LINEAR EQUATIONS

Solving Linear Equations in One Variable

Example 1 :

Solve for r : 

6r + 7  =  13 + 7r

Solution :

6r + 7 = 13 + 7r

Subtract 7r and 7 from each side.

- r  =  6

Multiply each side (-1).

r  =  - 6

So, the the value of r is -6.

Example 2 :

Solve for x :

13 - 4x  =  1 - x

Solution :

13 - 4x  =  1 - x

Add x to each side.

13 - 3x  =  1

Subtract 13 from each side.

- 3x  =  - 12

Divide each side by (-3)

x  =  4

So, the value of x is 4. 

Example 3 :

Solve for x : 

- 7x - 3x + 2  =  - 8x - 8 

Solution :

- 7x - 3x + 2  =  - 8x - 8

Combine the like term.

- 10x + 2  =  - 8x - 8

Add 8x to each side. 

- 2x + 2  =  - 8

Subtract 2 from each side. 

- 2x  =  - 10

Divide each side by (-2).

x  =  5. 

So, the value of x is 5.

Example 5 :

Solve for b : 

- 14 + 6b + 7 - 2b  =  1 + 5b 

Solution :

- 14 + 6b + 7 - 2b  =  1 + 5b 

Combine the like term.

4b - 7  =  1 + 5b

Subtract 5b from each side.

- b - 7  =  1

Add 7 to each side. 

- b  =  8

Multiply each side by (-1). 

b  =  - 8

So, the value of b is -8.

Example 5 :

Ana has 8 stamps. Together Ricky and Ana have 23 stamps. The equation 23 = r + 8 represents this situation, where r is the number of stamps Ricky has. solve the equation to find the number of stamps Ricky has.

Solution :

23 = r + 8

Subtracting 8 on both sides, 

23 - 8 = r

r = 15

So, the number of stamps is 15.

Example 6 :

Ryan's Rentals charge $40 per day plus $0.25 per mile. Road trips charges $25 per day plus $0.45 per mile.

For what number of miles is the daily cost of renting a car the same ? Write and solve the equation to represent this problem to check your solution.

Solution :

Let m be the number of miles.

Charge by Ryan's Rentals :

Cost per day + 0.25 per mile

= 40 + 0.25m

Charge by Road trips :

Cost per day + 0.25 per mile

= 25 + 0.45m

Cost should be the same, then

40 + 0.25m = 25 + 0.45m

40 - 25= 0.45m - 0.25m

15 = 0.20m

m = 15/0.20

m = 75

So, the required number of miles is 75.

Example 7 :

A rectangular bathroom with the side length shown is being covered with tiles. Where x is the length in feet of the square tiles. The perimeter is equal to 48x - 6. If each square foot of tile costs $8.49, what is the total cost to the tile of the bathroom ?

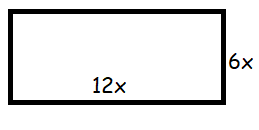
Solution :

Perimeter of the bathroom = 48 x - 6

Length of rectangle = 12x

Width of the rectangle = 6x

2(length + width) = 48x - 6

2(12x + 6x) = 48x - 6

2(18x) = 48x - 6

36x = 48x - 6

36x - 48x = -6

-12x = -6

x = 6/12

x = 0.5

Area of bathroom = length • width

= 12x • 6x

= 72x • x 

Applying the value of x, we get

= 72 • 0.5 • 0.5

= 18 square feet

Cost per square feet = $8.49

Required cost = 18(8.49)

= $152.82

Example 8 :

The triangle and square shown have the same perimeter. Solve the equation 3x + 4x + 5x = 4(x + 2) to find the value of x. Find the length of one side of the square.

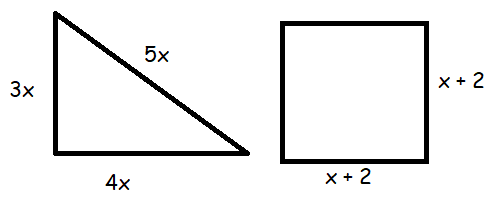
Solution :

3x + 4x + 5x = 4(x + 2)

12x = 4x + 8

12x - 4x = 8

8x = 8

x = 8/8

x = 1

Side length of square = x + 2

= 1 + 2

= 3

So, the side length of the square is 3 units.

Solving Linear Equations in Two Variables

We can follow the below methods to solve linear equations in two variables.

To know each of the methods given below in detail, please click on the links.

• Substitution method
• Elimination method
• Cross multiplication method
• Graphical method

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.