SOLVE A SYSTEM OF EQUATIONS BY GRAPHING

Solve the following systems of linear equations by graphing :

Example 1 :

y = x – 3

y = 3

Solution :

y = x – 3 :

The given equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.

When x = 0,

y = 0 - 3

= -3

(0, -3)

When x = 3,

y = 3 - 3

= 0

(3, 0)

Plot the points (0, -3), and (3, 0) on a xy-plane and connect them.

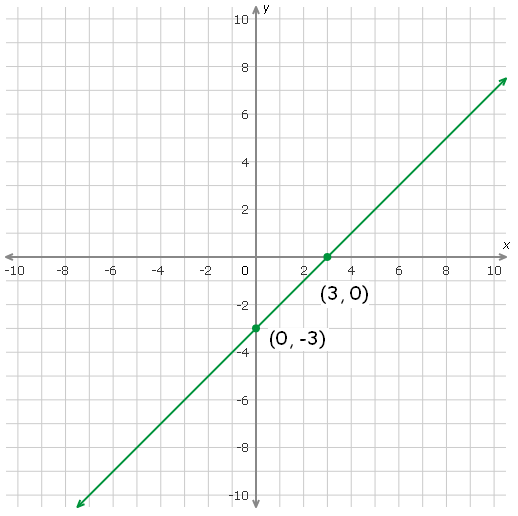
y = 3 :

This is the equation of a line parallel to x-axis through the value 3 on y-axis.

So, graph a straight parallel to x-axis through the value 3 on y-axis.

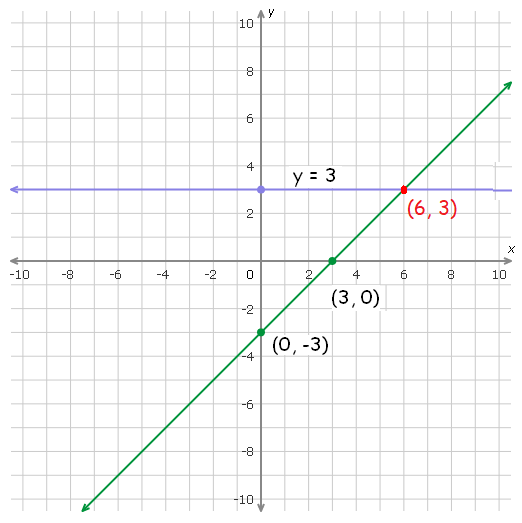
In the graph above, the two lines intersect at (6, 3).

So, 

x = 6 and y = 3

Example 2 :

2x + y - 2 = 0

5x + y + 1 = 0

Solution :

2x + y - 2 = 0 :

The given equation is not in slope-intercept form. Write the given equation is in slope intercept form.

2x + y - 2 = 0

Subtract 2x from both sides.

y - 2 = -2x

Add 2 to both sides.

y = -2x + 2

Now the equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.

When x = -1,

y = -2(-1) + 2

= 2 + 2

= 4

(-1, 4)

When x = 0,

y = -2(0) + 2

= 0 + 2

= 2

(0, 2)

Plot the points (-1, 4), and (0, 2) on a xy-plane and connect them.

5x + y + 1 = 0 :

The given equation is not in slope-intercept form. Write the given equation is in slope intercept form.

5x + y + 1 = 0

Subtract 5x and 1 from both sides.

y = -5x - 1

Now the equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.

When x = -1,

y = -5(-1) - 1

= 5 - 1

= 4

(-1, 4)

When x = 0,

y = -5(0) - 1

= 0 - 1

= -1

(0, -1)

Plot the points (-1, 4), and (0, -1) on a xy-plane and connect them.

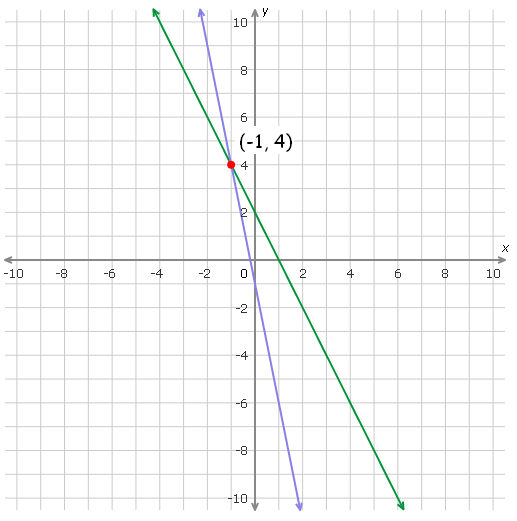
In the graph above, the two lines intersect at (-1, 4).

So, 

x = -1 and y = 4

Example 3 :

The graphs of two linear equations are shown

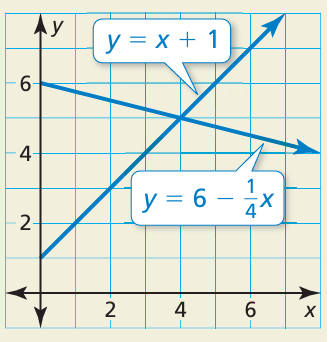
a. At what point do the lines appear to intersect?

b. Could you solve a system of linear equations by substitution to check your answer in part (a)? Explain.

Solution :

y = x + 1 -------(1)

y = 6 - (1/4)x-------(2)

a) By observing the graph, the point of intersection of the lines is (4, 5)

b)  To find the point of intersection, we may solve the system of equation using substitution method.

(1) = (2)

x + 1 = 6 - (1/4)x

x + (1/4)x = 6 - 1

(4x + 1x)/4 = 5

5x/4 = 5

x = 5(4/5)

x = 4

Applying x = 4 in (1), we get

y = 4 + 1

y = 5

The solution is (4, 5).

Example 4 :

Consider the equation x + 2 = 3x − 4.

a. Solve the equation using algebra.

b. Solve the system of linear equations y = x + 2 and y = 3x − 4 by graphing.

c. How is the linear system and the solution in part (b) related to the original equation and the solution in part (a)?

Solution :

a)

x + 2 = 3x − 4

x - 3x = -4 - 2

-2x = -6

x = 6/2

x = 3

Applying x = 3 in y = x + 2, we get

y = 3 + 2

y = 5

b. 

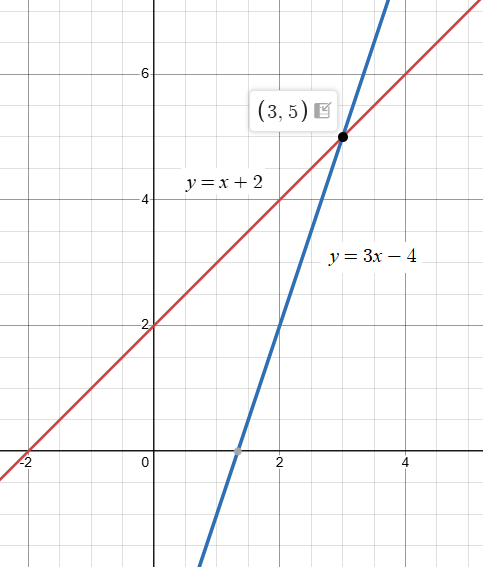
The point of intersection of the lines is (3, 5).

Example 5 :

Describe and correct the error in solving the system of linear equations.

The solution of the linear system y = 2x − 1 and y = x + 1 is x = 2.

Solution :

y = 2x − 1 ------(1)

y = x + 1 --------(2)

(1) = (2)

2x - 1 = x + 1

2x - x = 1 + 1

x = 2

Applying the value of x, we get

y = 2(2) - 1

y = 4 - 1

y = 3

By observing the graph the point of intersection of lines (2, 3).

So, there is no error.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.