CROSS MULTIPLICATION METHOD TO SOLVE LINEAR EQUATIONS IN TWO VARIABLES

This is one of the methods we use to solve system of linear equations.

Let us consider the following system of linear equations.

a₁x + b₁y + c₁ = 0

a₂x + b₂y + c₂ = 0

We have to write the coefficients of the equations and do cross multiplication as shown below.

We write the coefficient of y and constant term and two more columns by repeating the coefficients of x and y as follows.

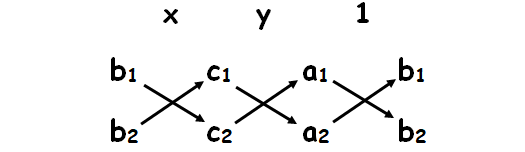
The result is given by

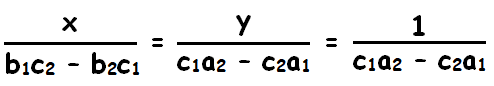
The solution is

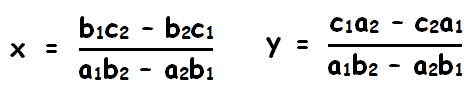
Example 1 :

Solve the following system of equations using cross multiplication method :

2x + 7y - 5 = 0

-3x + 8y = -11

Solution :

First we have to change the given linear equations in the form a₁x + b₁y + c₁  =  0, a₂x + b₂y + c₂  =  0.

2x + 7y - 5  =  0

-3x + 8y + 11  =  0

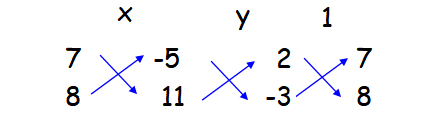
x/(77 + 40) = y/(15 - 22) = 1/[16 + 21]

x/117 = y/(-7) = 1/37

Therefore the solution is (117/37, -7/37).

Example 2 :

Solve the following system of equations using cross multiplication method :

3x + 4y = 24

20x - 11y = 47

Solution :

Write the given equations in the form of

a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0

3x + 4y - 24 = 0 ----(1)

20x - 11y - 47 = 0 ----(2)

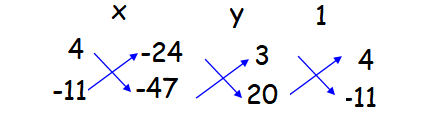
x/(-188 - 264) = y/(-480 - (-141)) = 1/(-33 - 80)

x/(-452) = y/(-480+141)) = 1/(-33-80)

x/(-452) = y/(-339) = 1/(-113)

Therefore solution is (4, 3).

Example 3 :

The sum of the digits of a two-digit number is 9. If 27 is added to it, the digits of the number get reversed. The number is

(A) 25      (B) 72      (C) 63     (D) 36

Solution :

Let xy be the required two digit number.

x + y = 9

x + y - 9 = 0 -----(1)

xy + 27 = yx

Writing in expanded form, we get

10x + 1y + 27 = 10y + 1x

10x - x + 1y - 10y + 27 = 0

9x - 9y - 27 = 0

Dividing by 9, we get

x - y - 3 = 0 -----(2) 

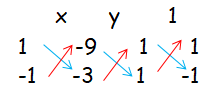
x/(-3 - 9) = y/(-9 + 3) = 1/(-1 - 1)

x/(-12) = y/(-6) = 1/(-2)

So, the values of x and y are 6 and 3 respectively. The required two digit number is 63.

Example 4 :

The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son’s age. The present ages, in years, of the son and the father are, respectively

(A) 4 and 24     (B) 5 and 30

(C) 6 and 36     (D) 3 and 24

Solution :

Let x be the son's age.

Father's age = 6x

Four years after :

Son's age = x + 4

Father's age = 4(x + 4)

6x + 4 = 4(x + 4)

6x + 4 = 4x + 16

6x - 4x = 16 - 4

2x = 12

x = 6 (son's age)

6x = 6(6) ==> 36 (father's age)

So, option c is correct.

Example 5 :

If 2x + y = 23 and 4x – y = 19, find the values of 5y – 2x and (y/x) – 2

Solution :

2x + y = 23

2x + y - 23 = 0 ----(1)

4x – y = 19

4x - y - 19 = 0 ------(2)

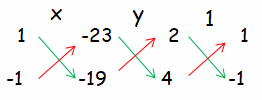
x/(-19 - 23) = y/(-92 + 38) = 1/(-2 - 4)

x/(-42) = y/(-54) = 1/(-6)

To find the values of 5y – 2x and (y/x) – 2, we apply the values of x and y.

Example 6 :

Two years ago, Salim was thrice as old as his daughter and six years later, he will be four years older than twice her age. How old are they now?

Solution :

Let x be the present age of daughter and y be the present age of Salim.

Two years ago :

Age of daughter = x - 2

Age of salim = y - 2

(y - 2) = 3(x - 2)

y - 2 = 3x - 6

3x - y = -2 + 6

3x - y = 4

3x - y - 4 = 0 -------(1)

y + 6 = 2(x + 6) + 4

y + 6 = 2x + 12 + 4

2x - y + 16 - 6

2x - y + 10 = 0 -------(2)

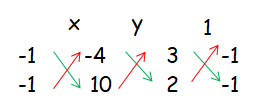
x/(-10 - 4) = y/(-8 - 30) = 1/(-3 + 2)

-x/14 = -y/38 = -1

-x/14 = -1 and -y/38 = -1

x = 14 and y = 38

So, age of daughter is 14 years and age of father is 38 years.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.