PROBLEMS USING THE OPERATOR SET DIFFERENCE

Set difference is one of the important operations on sets which can be used to find the difference between two sets.  

Let us discuss this operation in detail. 

Let X and Y be two sets.

Now, we can define the following new set.

X \ Y  =  {z | z ∈ X but z ∉  Y}

(That is z must be in  X and must not be in Y)

X \ Y is read as "X difference Y"

Now that X \ Y contains only elements of X which are not in Y and the figure given below illustrates this. 

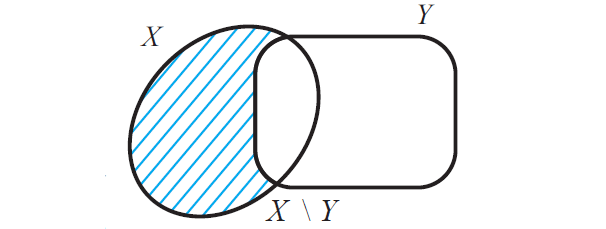
Some authors use A - B for A \ B. We shall use the notation A \ B which is widely used in mathematics for set difference. 

Question 1 :

For A  =  {5, 10, 15, 20} B  =  {6, 10, 12, 18, 24} and C  =  {7, 10, 12, 14, 21, 28} verify whether A\(B\C) = (A\B)\C. Justify your answer.

Solution :

A  =  {5, 10, 15, 20}

B  =  {6, 10, 12, 18, 24}

C  =  {7, 10, 12, 14, 21, 28}

L.H.S

A\(B\C)

(B\C)  =  {6, 10, 12, 18, 24}\{7, 10, 12, 14, 21, 28}

  =  {6, 18, 24}

A\(B\C)  =  {5, 10, 15, 20}\{6, 18, 24}

  =  {5, 10, 15, 20}  ---(1)

(A\B)  =  {5, 10, 15, 20}\{6, 10, 12, 18, 24}

  =  {5, 15, 20}

(A\B)\C  =  {5, 15, 20} \ {7, 10, 12, 14, 21, 28}

  =  {5, 15, 20}   --- (2)

A\(B\C)  ≠  (A\B)\C

Question 2 :

Let A  =  {-5, -3, -2, -1} B  =  {-2, -1, 0} and C  =  {-6, -4, -2}. Find A\(B\C) and (A\B)\C. What can we conclude about set difference operation?

Solution :

A  =  {-5, -3, -2, -1} B  =  {-2, -1, 0} and C  =  {-6, -4, -2}

L.H.S

A\(B\C)

(B\C)  =  {-2, -1, 0}\{-6, -4, -2}

  =  {-1,0}

A\(B\C)  =  {-5, -3, -2, -1}\{-1, 0}

  =  {-5, -3, -2} ---- (1)

R.H.S

(A\B)\C

(A\B)  =  {-5, -3, -2, -1}\{-2, -1, 0}

  =  {-5, -3}

(A\B)\C = {-5,-3} \ {-6,-4,-2}

  =  {-5, -3}  -----(2)

(1) ≠ (2)

A\(B\C) ≠ (A\B)\C

Related pages

• Representation of Set 
• Types of set
• Disjoint sets 
• Power Set
  
• Operations on Sets
• Laws on set operations
• More Laws
• Venn diagrams
• Set word problems
• Relations and functions

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.