OPERATIONS ON SETS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
When two or more sets are combined together to form another set under some given conditions, then operations on sets are carried out.
The important operations on sets are.
1. Union
2. Intersection
3. Set difference
4. Symmetric difference
5. Complement
6. Disjoint sets
Let us discuss the above operations in detail one by one.
Union
Let X and Y be two sets.
Now, we can define the following new set.
X u Y = {z | z ∈ X or z ∈ Y}
(That is, z may be in X or in Y or in both X and Y)
X u Y is read as "X union Y"
Now that X u Y contains all the elements of X and all the elements of Y and the figure given below illustrates this.
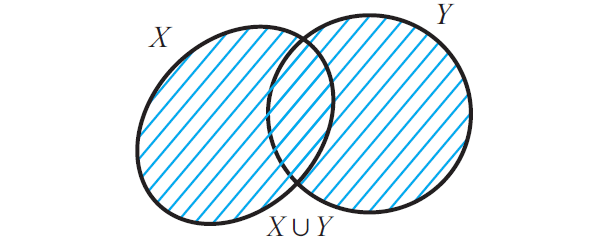
It is clear that X ⊆ X u Y and also Y ⊆ X u Y.
Intersection
Let X and Y be two sets.
Now, we can define the following new set.
X n Y = {z | z ∈ X and z ∈ Y}
(That is z must be in both X and Y)
X n Y is read as "X intersection Y"
Now that X n Y contains only those elements which belong to both X and Y and the figure given below illustrates this.
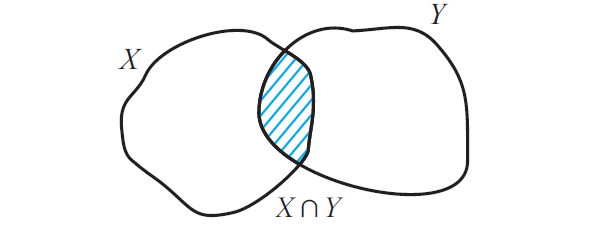
It is trivial that that X n Y ⊆ X and also X n Y ⊆ Y.
Set Difference
Let X and Y be two sets.
Now, we can define the following new set.
X\Y = {z | z ∈ X but z ∉ Y}
(That is z must be in X and must not be in Y)
X\Y is read as "X difference Y"
Now that X \ Y contains only elements of X which are not in Y and the figure given below illustrates this.
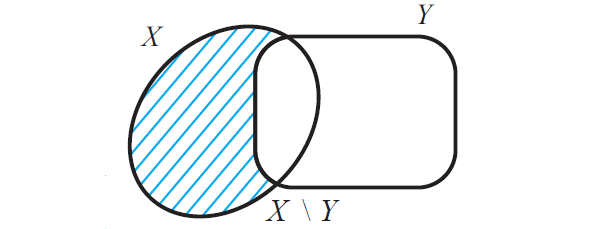
Some authors use A - B for A\B. We shall use the notation A\B which is widely used in mathematics for set difference.
Symmetric Difference
Let X and Y be two sets.
Now, we can define the following new set.
X Δ Y = (X\Y) u (Y\X)
X Δ Y is read as "X symmetric difference Y"
Now that X Δ Y contains all elements in X u Y which are not in X n Y and the figure given below illustrates this. .
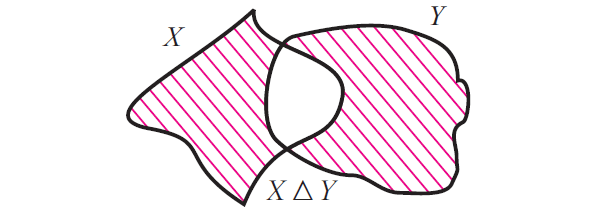
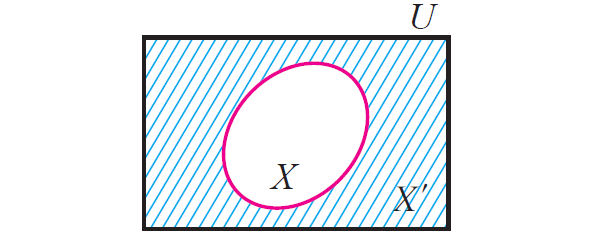
Complement of a Set
If X ⊆ U, where U is a universal set, then U \ X is called the compliment of X with respect to U. If underlying universal set is fixed, then we denote U \ X by X' and it is called compliment of X.
X' = U\X
or
Xc = U\X
The difference set set A \ B can also be viewed as the compliment of B with respect to A.
Disjoint Sets
Two sets X and Y are said to be disjoint if they do not have any common element. That is, X and Y are disjoint if
X n Y = ∅
It is clear that n(A u B) = n(A) + n(B), if A and B are disjoint finite set.
Using Operations on Sets
Consider the following sets.
U = {1, 2, 3, 4, ......., 100}
A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
B = {1, 2, 4, 6, 7, 8, 12, 15}
C = {-2, -1, 0, 1, 3, 5, 7}
Now, let us find the following.
(i) AuB :
AuB = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 15}
(ii) BnC :
BnC = {1, 7}
(iii) A\C :
A/C = {2, 4, 6, 8, 9, 10, 11}
(iv) A Δ C :
A Δ C = (A\C) u (C\A)
A Δ C = {2, 4, 6, 8, 9, 10, 11} u {-2, -1, 0}
A Δ C = {-2, -1, 0, 2, 4, 6, 8, 9, 10, 11}
(v) Ac :
Ac = U\A
Ac = U - A
Ac = {13, 14, 15, ......., 100}
Let us list out some useful results.
Let U be a universal set and A, B are subsets of U.
Then the following hold :
(i) A\B = AnBc
(ii) B\A = BnAc
(iii) A\B = A ----> AnB = ∅
(iv) (A\B)uB = AuB
(v) (A\B)nB = ∅
(vi) (A\B)u(B\A) = (AuB)\(AnB)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 29, 25 04:21 AM
10 Hard SAT Math Questions (Part - 38) -
10 Hard SAT Math Questions (Part - 39)
Dec 28, 25 11:20 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 41)
Dec 28, 25 06:05 PM
10 Hard SAT Math Questions (Part - 41)

