TYPES OF SETS

The concept of set is vital to mathematical thought and is being used in almost every branch of mathematics. In mathematics, sets are convenient because all mathematical structures can be regarded as sets.

Here, we are going to see the different types of sets.

Empty Set or Null Set

A set containing no elements is called the empty set or null set or void set.

Reading notation :

So, it is denoted by {  } or ∅. 

For example,

Consider the set A  =  {x : x < 1, x ∈ N}

There is no natural number which is less than 1. 

Therefore, A  =  {  }, n(A)  =  0.  

Note : 

The concept of empty set plays a key role in the study of sets just like the role of the number zero in the study of number system.

Finite Set

If the number of elements in a set is zero or finite, then the set is called a finite set.

For example,

(i)  Consider the set A of natural numbers between 8 and 9.

There is no natural number between 8 and 9.

So, A  =  {  } and n(A) = 0.

Hence, A is a finite set.  

(ii)  Consider the set X = {x : x is an integer and -1 ≤ x ≤ 2}

So, X  =  {-1, 0, 1, 2} and n(X)  = 4  

Hence, X is a finite set. 

Note : 

The cardinal number of a finite set is finite.

Infinite Set

A set is said to be an infinite set if the number of elements in the set is not finite.

For example, 

Let W  =  The set of all whole numbers .

That is, W  =  {0, 1, 2, 3, ......................}

The set of all whole numbers contain infinite number of elements.

Hence, W is an infinite set. 

Note : 

The cardinal number of an infinite set is not a finite number. 

Singleton Set

A set containing only one element is called a singleton set. 

For example, 

Consider the set A  =  {x : x is an integer and 1 < x < 3}.

So, A  =  { 2 }. That is, A has only one element.

Hence, A is a singleton set. 

Note :

{0} is not null set. Because it contains one element.

That is "0". 

Equivalent Set

Two sets A and B are said to be equivalent if they have the same number of elements.

In other words, A and B are equivalent if n(A)  =  n(B).

Reading notation :

"A and B are equivalent" is written as A ≈ B

For example, 

Consider A  =  { 1, 3, 5, 7, 9 } and B  =  { a, e, i, o, u }

Here n(A)  =  n(B)  =  5

Hence, A and B are equivalent sets. 

Equal Sets

Two sets A and B are said to be equal if they contain exactly the same elements, regardless of order.

Otherwise the sets are said to be unequal.

In other words, two sets A and B are said to be equal if

(i) every element of A is also an element of B and

(ii) every element of B is also an element of A.

Reading notation :

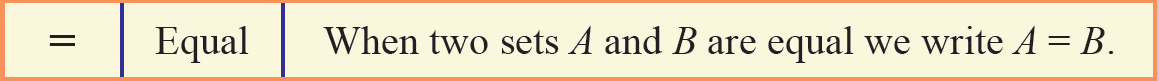
For example, 

Consider A  =  {a, b, c, d} and B  =  {d, b, a, c}.

Set A and set B contain exactly the same elements.

And also  n(A)  =  n(B)  =  4.

Hence, A and B are equal sets.

Note :

If n(A) = n(B), then the two sets A and B need not be equal. Thus, equal sets are equivalent but equivalent sets need not be equal.

Subset

A set X is a subset of set Y if every element of X is also an element of Y.

In symbol we write 

x ⊆ y

Reading Notation :

Read ⊆ as "X is a subset of Y" or "X is contained in Y".

Read ⊈ as "X is a not subset of Y" or "X is not contained in Y".

Proper subset

A set X is said to be a proper subset of set Y if X ⊆ Y and X ≠ Y. 

In symbol, we write X ⊂ Y

Reading notation :

Read X ⊂ Y as "X is proper subset of Y".

The figure given below illustrates this.

Power Set

The set of all subsets of A is said to be the power set of the set A.

Reading notation :

The power set of A is denoted by P(A).

Super Set

A set X is said to be a proper subset of set Y if X ⊆ Y and X ≠ Y. 

In symbol, we write X ⊂ Y

Here,

Y is called super set of X

Formula to Find Number of Subsets

If A is the given set and it contains "n" number of elements, we can use the following formula to find the number of subsets.

Number of subsets  =  2ⁿ

Formula to find the number of proper subsets :

Number of proper subsets  =  2^n-1

Cardinality of Power Set

We already know that the set of all subsets of A is said to be the power set of the set A and it is denoted by P(A).

If A contains "n" number of elements, then the formula for cardinality of power set of A is

n[P(A)]  =  2ⁿ

Note :

Cardinality of power set of A and the number of subsets of A are same.

Null Set is a Subset or Proper Subset

Null set is a proper subset for any set which contains at least one element.  

For example, let us consider the set A  =  {1}.

It has two subsets. They are { } and {1}. 

Here null set is proper subset of A. Because null set is not equal to A.  

If Null Set is a Super Set

If null set is a super set, then it has only one subset. That is { }. 

More clearly, null set is the only subset to itself. But it is not a proper subset.

Because, { }  =  { }.

Therefore, A set which contains only one subset is called null set.  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.