PRACTICE PROBLEMS ON UNION INTERSECTION AND COMPLEMENT
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Union of two sets :
The union of two sets contains all the elements contained in either set (or both sets).
The union is notated A ⋃ B.
More formally, x ∊ A ⋃ B if x ∊ A or x ∊ B (or both)
Intersection of two sets :
The intersection of two sets contains only the elements that are in both sets.
The intersection is notated A ⋂ B.
More formally, x ∊ A ⋂ B if x ∊ A and x ∊ B
Complement of two sets :
The complement of a set A contains everything that is not in the set A.
The complement is notated A’, or Ac, or sometimes ~A.
Question 1 :
If A ⊂ B,then show that A U B = B (use venn diagram)
Solution :
Since A is the subset of B we have to draw a small circle A inside the large circle B.
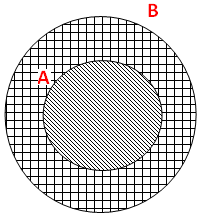
A U B = B
Question 2 :
If A ⊂ B, then find A∩B and A\B (use venn diagram)
Solution :
Since A is the subset of B we have to draw a small circle A inside the large circle B.
A∩B means we have to shade common part of A and B. From this we will get
A∩B = A

Question 3 :
Let P = {a, b, c}, Q = {g, h, x, y} and R = {a, e, f, s}. Find the following
(i) P\R (ii) Q∩R (iii) R\(P∩Q)
Solution :
(i) To find P\R we have to choose the common elements from both P and R and we have to write remaining elements in P.
P\R = {a, b, c} \ {a, e, f, s}
= {b, c}
(ii) To find Q∩R we have to write the common elements in Q and R.
Q∩R = {g, h, x, y} ∩ {a, e, f, s}
there is no common elements in both Q and R
Q∩R = Ø
(iii) R\(P∩Q)
P∩Q = {a, b, c} ∩ {g, h, x, y}
There is no common elements in both P and Q
P∩Q = Ø
R\(P∩Q) = {a, b, c}\Ø
= {a,b,c}
Question 4 :
If A = 4, 6, 7, 8, 9} , B = {2, 4, 6} and C = {1, 2, 3, 4, 5, 6}, then find
(i) AU(B∩C) (ii) A∩(BUC) (iii) A\(C\B)
Solution :
(i) AU(B∩C)
(B∩C) = {2, 4, 6} ∩ {1, 2, 3, 4, 5, 6}
= {2, 4, 6}
AU(B∩C) = {4, 6, 7, 8, 9} U {2, 4, 6}
= {2, 4, 6, 7, 8, 9}
(ii) A∩(BUC)
(BUC) = {2, 4, 6} U {1, 2, 3, 4, 5, 6}
= {1, 2, 3, 4, 5, 6}
A∩(BUC) = {4, 6, 7, 8, 9} ∩ {1, 2, 3, 4, 5, 6}
= {4, 6}
(iii) A\(C\B)
C\B = {1, 2, 3, 4, 5, 6}\{2, 4, 6}
= {1, 3, 5}
A\(C\B) = {4, 6, 7, 8, 9}\{1, 3, 5}
= {4, 6, 7, 8, 9}
Related topics
- Representation of Set
- Types of set
- Disjoint sets
- Power Set
- Operations on Sets
- Laws on set operations
- More Laws
- Venn diagrams
- Set word problems
- Relations and functions
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
SAT Math Challenge Problems
Feb 10, 26 04:49 AM
SAT Math Challenge Problems -
How to Solve Challenging Math Problems in SAT
Feb 10, 26 03:14 AM
How to Solve Challenging Math Problems in SAT -
The Hidden Patterns in Hard SAT Math Questions
Feb 09, 26 06:45 PM
The Hidden Patterns in Hard SAT Math Questions