RELATIONS AND FUNCTIONS CLASS 11 WORKSHEET

(1)  Suppose that 120 students are studying in 4 sections of eleventh standard in a school. Let A denote the set of students and B denote the set of the sections. Define a relation from A to B as “x related to y if the student x belongs to the section y”. Is this relation a function? What can you say about the inverse relation? Explain your answer.              Solution

(2)  Write the values of f at −4, 1,−2, 7, 0 if

Solution

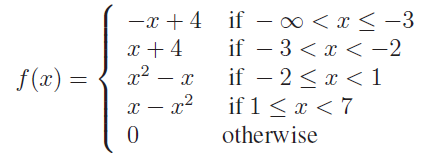
(3)  Write the values of f at −3, 5, 2,−1, 0 if

Solution

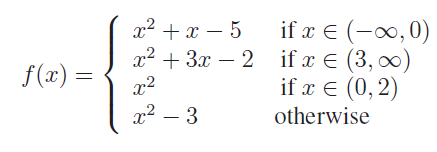
(4)  State whether the following relations are functions or not. If it is a function check for one-tooneness and ontoness. If it is not a function, state why?

(i) If A = {a, b, c} and f = {(a, c), (b, c), (c, b)}; (f : A → A).

(ii) If X = {x, y, z} and f = {(x, y), (x, z), (z, x)}; (f : X → X).           Solution

(5)  Let A = {1, 2, 3, 4} and B = {a, b, c, d}.

Give a function from A → B for each of the following:

(i) neither one-to-one nor onto.

(ii) not one-to-one but onto.

(iii) one-to-one but not onto.

(iv) one-to-one and onto.               Solution

(6)  Find the domain of 1 / (1 − 2 sinx)        Solution

(7)  Find the largest possible domain of the real valued function f(x)  =  √(4 - x²)/ √(x² - 9)        Solution

(8) Find the range of the function

1 / (2 cos x − 1)           Solution

(9)  Show that the relation xy = −2 is a function for a suitable domain. Find the domain and the range of the function.        Solution

(10)  If f, g : R → R are defined by f(x) = |x| + x and g(x) = |x| − x, find g ◦ f and f ◦ g.         Solution

(11)  If f, g, h are real valued functions defined on R, then prove that (f + g) ◦ h = f◦h + g ◦ h. What can you say about f ◦ (g + h) ? Justify your answer.       Solution

(12)  If f : R → R is defined by f(x) = 3x − 5, prove that f is a bijection and find its inverse.       Solution

(13)  The weight of the muscles of a man is a function of his body weight x and can be expressed as W(x) = 0.35x. Determine the domain of this function.       Solution

(14)  The distance of an object falling is a function of time t and can be expressed as s(t) = −16t². Graph the function and determine if it is one-to-one.       Solution

(15)  The total cost of airfare on a given route is comprised of the base cost C and the fuel surcharge S in rupee. Both C and S are functions of the mileage m; C(m) = 0.4m + 50 and S(m) = 0.03m. Determine a function for the total cost of a ticket in terms of the mileage and find the airfare for flying 1600 miles.                     Solution

(16)  A salesperson whose annual earnings can be represented by the function A(x) = 30, 000 + 0.04x, where x is the rupee value of the merchandise he sells. His son is also in sales and his earnings are represented by the function S(x) = 25, 000 + 0.05x. Find (A + S)(x) and determine the total family income if they each sell Rupees 1, 50, 00, 000 worth of merchandise.        Solution

(17)  The function for exchanging American dollars for Singapore Dollar on a given day is f(x) = 1.23x, where x represents the number of American dollars. On the same day the function for exchanging Singapore Dollar to Indian Rupee is g(y) = 50.50y, where y represents the number of Singapore dollars. Write a function which will give the exchange rate of American dollars in terms of Indian rupee.               Solution

(18)  The owner of a small restaurant can prepare a particular meal at a cost of Rupees 100. He estimates that if the menu price of the meal is x rupees, then the number of customers who will order that meal at that price in an evening is given by the function D(x) = 200−x. Express his day revenue, total cost and profit on this meal as functions of x.               Solution

(19)  The formula for converting from Fahrenheit to Celsius temperatures is y = (5x/9) − (160/9). Find the inverse of this function and determine whether the inverse is also a function               Solution

(20)  A simple cipher takes a number and codes it, using the function f(x) = 3x−4. Find the inverse of this function, determine whether the inverse is also a function and verify the symmetrical property about the line y = x (by drawing the lines).                  Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.