PRACTICE QUESTIONS ON RELATION FOR GRADE 11

Question 1 :

Suppose that 120 students are studying in 4 sections of eleventh standard in a school. Let A denote the set of students and B denote the set of the sections. Define a relation from A to B as “x related to y if the student x belongs to the section y”. Is this relation a function? What can you say about the inverse relation? Explain your answer.

Solution :

A be the set of students and B be the set of sections.

Every student in set A will be belonging at least any one of the classes of set B. Hence the above relation is a function.

Now let us consider about inverse relation. During the inverse relation, each section will have more than 1 students, which are given one to many relation.

That is, the section C1 will have more than 1 students. So we have to draw arrow mark from C1 to more than one student in set A. Hence it is not a function.

Question 2 :

Write the values of f at −4, 1,−2, 7, 0 if

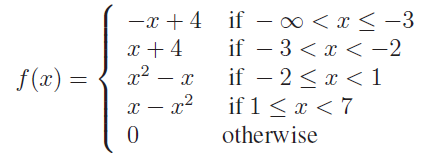
Solution :

(i) x = -4,

-4 lies in the interval (-∞, -3]

f(x)  =  -x + 4

x =  -4

f(-4)  =  - (-4) + 4  =  8

(ii) x = 1,

1 lies in the interval [1, 7)

f(x)  =  x - x² 

f(1)  =  1 - 1²   =  0

(iii) x = -2,

-2 lies in the interval [-2, 1)

f(x)  =  x² - x

f(-2)  =  (-2)² - (-2)

  =  4 + 2

=  6

(iv) x = 7,

 Do not lie in the given intervals. Hence f(7) is 0.

(v) x = 0,

0 lies in the interval [-2, 1)

f(x)  =  x² - x

f(0)  =  0² - 0  =  0 

Question 3 :

Write the values of f at −3, 5, 2,−1, 0 if

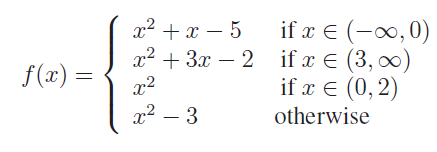
Solution :

(i) x = -3,

-3 lies in the interval (-∞, 0)

f(x)  =  x² + x - 5

f(-3)  =  (-3)² + (-3) - 5

=  9 - 3 - 5

f(-3)  =  1

(ii) x = 5

5 lies in the interval (3, ∞)

f(x)  =  x² + 3x - 2

f(5)  =  5² + 3(5) - 2

=  25 + 15 - 2

=  38

(iii) x = 2 

Do not lie in the given intervals. Hence f(2) is 0.

(iv) x = -1 

-1 lies in the interval (-∞, 0)

f(x)  =  x² + x - 5

f(-1)  =  (-1)² + (-1) - 5

=  1 - 1 - 5

=  1 - 6

=  -5

(v) x = 0 

Do not lie in the given intervals. Hence f(0) is 0.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.