HOW TO CHECK IF THE GIVEN RELATION IS FUNCTION

Problems 1-2 : State whether the following relations are functions or not. If it is a function, check for one-to-one onto. If it is not a function, state why?

Problem 1 :

A = {a, b, c} and f = {(a, c), (b, c), (c, b)}; (f : A ---> A).

Solution :

In order to check, if the given relation form a function, it has to satisfy the following conditions.

(i) Domain of f = {a, b, c} = set A.

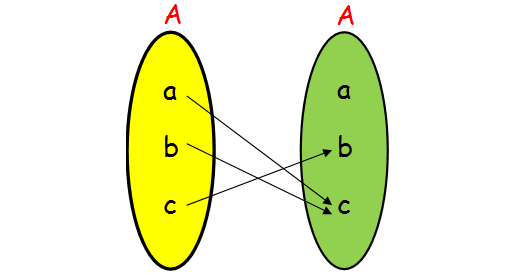
(ii)  For each x ∊ A, there is only one y ∊ A. Hence it is a function.

Not One to One :

If it is one to one function, then each elements of A will be associated with different elements of A. Here the elements a and b are associated with c.

Not Onto :

The element a is not associated with any of the elements, hence it is not onto.

Problem 2 :

If X = {x, y, z} and f = {(x, y), (x, z), (z, x)}; (f : X ---> X).

Solution :

(i)  Domain of f  =  {x, z}  ≠ set X

Hence it is not a function.

Problem 3 :

Let A = {1, 2, 3, 4} and B = {a, b, c, d}.

Give a function from A ---> B for each of the following :

(i) neither one-to-one nor onto.

(ii) not one-to-one but onto.

(iii) one-to-one but not onto.

(iv) one-to-one and onto.

Solution :

(i) neither one-to-one nor onto.

First let us draw a arrow diagram under the given condition, then write the relation from the arrow diagram.

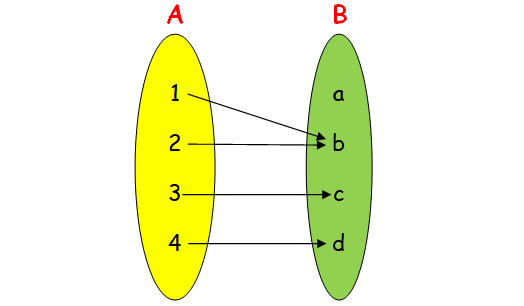
It is not one to one, because 1 and 2 are having same image b.

It is not onto, because a is not having preimage.

Hence the required relation is {(1, b) (2, b) (3, c) (4, d)}

(ii) not one-to-one but onto.

Inorder to prove it is an onto function, every element of B should have atleast one preimage. If we associate each elements of B with A, we will get one to one function or not a function. 

Hence it is not possible.

(iii) one-to-one but not onto

To prove it is an one to function, we need to associate every element of A with different elements of B. By doing this we will not get onto function. Hence it is not possible.

(iv) one-to-one and onto.

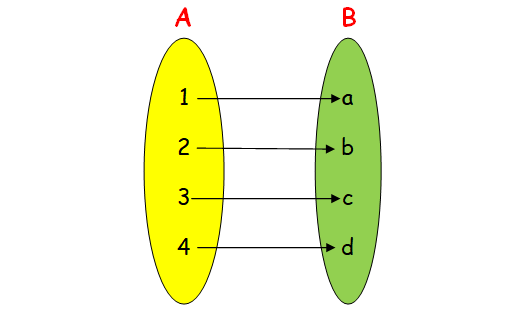
To prove it is an one to function, we need to associate every element of A with different elements of B. It is also an onto function.

Hence the required relation is {(1, a) (2, b) (3, c) (4, d)}.

Determine if the following relations are functions. Then state the domain and range.

Problem 4 :

{(1, -2) (-2, 0) (-1, 2) (1, 3)}

Solution :

Is it a function :

No, because the input 1 is having two outputs -2 and 3. Then, it is not a function.

Domain :

{-2, -1, 1}

Range :

{-2, 0, 3}

Problem 5 :

{(1, 1) (2, 2) (3, 5) (4, 10)(5, 15)}

Solution :

Is it a function :

Yes, each input is having different, no inputs is having the same outputs. Then, it is a function.

Domain :

{1, 2, 3, 4, 5}

Range :

{1, 2, 5, 10, 15}

Write each of the following as relation, state the domain and range and determine if it is function or not.

Problem 6 :

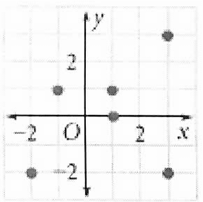
Solution :

Writing down as set of ordered pairs,

Relation :

(-1, 1)(-2, -2) (1, 0) (1, 1) (3, 3) and (3, -2).

Domain : 

{-2, -1, 1, 3}

Range :

{-2, 1, 0, 3}

Function or not :

Here 1 is the input which is having two different outputs, then it is not a function.

Problem 7 :

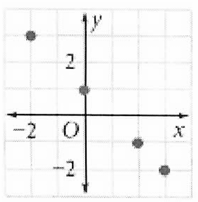
Solution :

Writing down as set of ordered pairs,

Relation :

(-2, 3) (0, 1) (1, -1) (3, -2)

Domain : 

{-2, 0, 1, 3}

Range :

{-2, -1, 1, 3}

Function or not :

Here 1 is the input which is having two different outputs, then it is not a function.

Problem 8 :

Rewrite the relation given in the mapping diagram as a scatterplot.

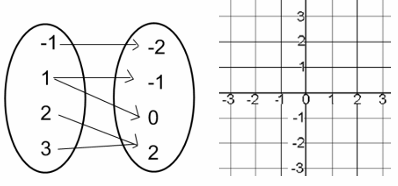
Is the relation also a function?

Solution :

Writing the mapping diagram as set of ordered pairs, we get

(-1, -2) (1, -1) (1, 0) (2, 2) (3, 2)

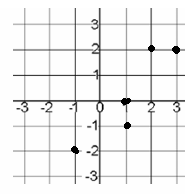
Here 1 is the input 1 is associated with two different outputs -1 and 0. Then it is not a function.

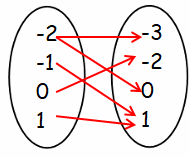
Problem 9 :

Rewrite the relation given in the scatter plot as a mapping diagram.

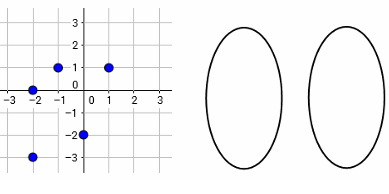
Is the relation also a function?

Solution :

Writing the points shown in the scatter plot as set of ordered pairs,

(-1, 1) (-2, 0) (0, -2) (-2, -3) (1, 1)

Determine if each graph shows a function or a relation only. Then identify the domain and range.

Problem 10 :

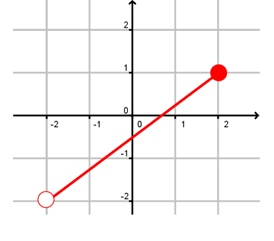
Solution :

By using vertical line test, it will intersect the curve maximum at one point. So, it is function.

Since it is continous function, domain and range can be represented by using interval notation.

• Domain (-2, 2]
• Range [-2, 1]

Problem 11 :

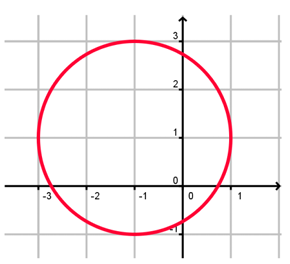
Solution :

By using vertical line test, it will intersect the curve maximum at two points. So, it is not a function.

• Domain [-3, 1]
• Range [-1, 3]

Problem 12 :

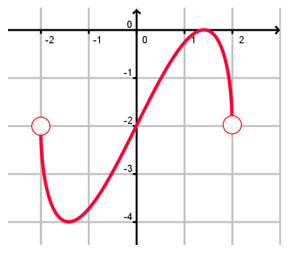
Solution :

By using vertical line test, it will intersect the curve maximum at one point. So, it is a function.

• Domain (-2, 2)
• Range (-4, 0)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.