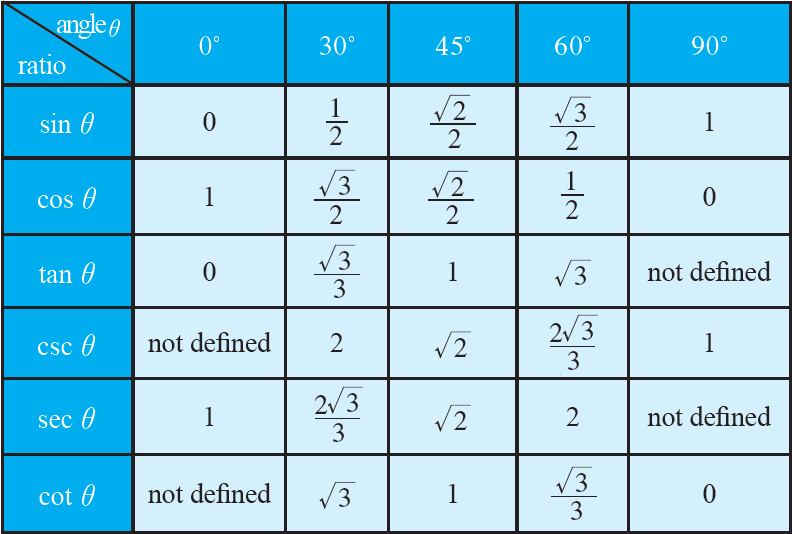
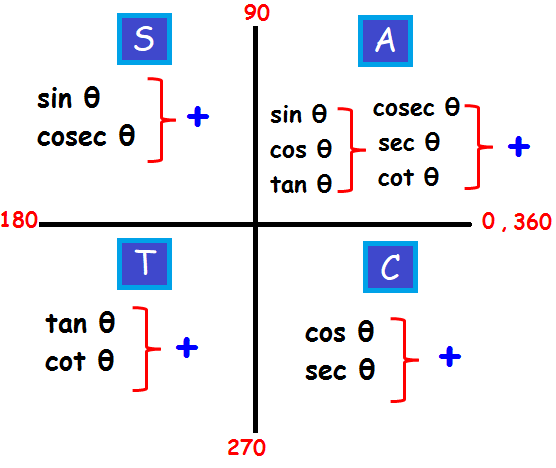
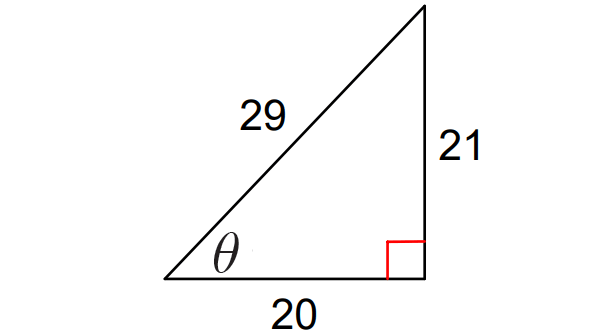
SOLVING PROBLEMS USING USING SECTION FORMULA
We studied bisection and trisection of a given line segment. These are only particular cases of the general problem of dividing a line segment joining two points (x1, y1) and (x2 , y2) in the ratio m : n.
Section formula (internally) :
((mx2 + nx1)/(m + n), (my2 + ny1)/(m + n))
Section formula (externally) :
((mx2 - nx1)/(m - n), (my2 - ny1)/(m - n))
Problem 1 :
Find the coordinates of the point which divides the line segment joining the points A(4,−3) and B(9, 7) in the ratio 3:2.
Solution :
= (mx2 + nx1)/(m + n), (my2 + ny1)/(m + n)
= (3(9) + 2(4))/(3 + 2), (3(7) + 2(-3))/(3 + 2)
= (27 + 8)/5, (21 - 6))/5
= 35/5, 15/5
= (7, 3)
Problem 2 :
In what ratio does the point P(2,−5) divide the line segment joining A(−3, 5) and B(4, −9).
Solution :
= (mx2 + nx1)/(m + n), (my2 + ny1)/(m + n)
= (m(4) + n(-3))/(m + n), (m(-9) + n(5))/(m + n)
(4m - 3n)/(m + n), (-9m + 5n)/(m + n) = (2, -5)
By equating x and y-coordinates, we get
(4m - 3n)/(m + n) = 2
4m - 3n = 2m + 2n
4m - 2m = 2n + 3n
2m = 5n
m/n = 5/2
m : n = 5 : 2
Hence the required ratio is 5 : 2
Problem 3 :
Find the coordinates of a point P on the line segment joining A(1, 2) and B(6, 7) in such a way that AP = (2/5) AB.
Solution :
AP = (2/5) AB.
AP/AB = 2/5
AB = 5
AP + PB = AB
2 + PB = 5
PB = 5 - 2 = 3
So, the point P divides the line segment in the ratio 2 : 3.
A(1, 2) and B(6, 7)
P = (2(6) + 3(1))/(2 + 3), (2(7) + 3(2))/(2 + 3)
P = (15/5, 20/5)
P = (3, 4)
Hence the required point is (3, 4).
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Trigonometry Sum and Difference Identities
May 07, 24 09:17 AM
Trigonometry Sum and Difference Identities - Concept - Solved Problems -
Trigonometry Even and Odd Iidentities
May 05, 24 12:25 AM
Trigonometry Even and Odd Iidentities -
SOHCAHTOA Worksheet
May 03, 24 08:50 PM
SOHCAHTOA Worksheet