PRACTICE PROBLEMS ON SIMILAR TRIANGLES
(1) Find the unknown values in each of the following figures. All lengths are given in centimeters (all measures are not in scale)
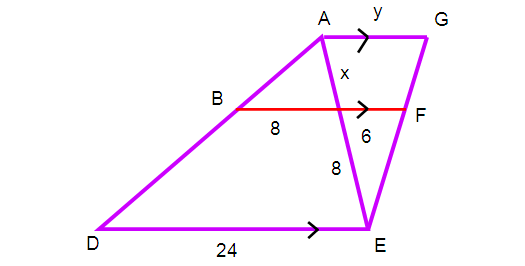
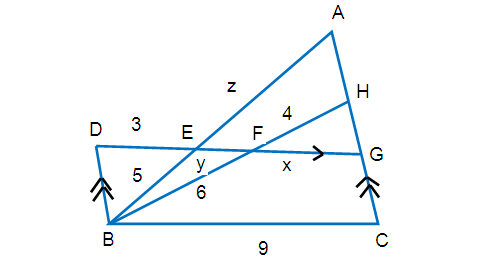
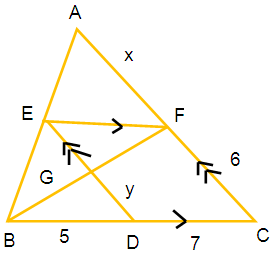
(2) A girl is
in the beach with her father. She spots a swimmer drowning. She shouts to her
father who is 50 m due west of her. Her father is 10 m nearer to a boat than
the girl. If her father uses the boat to reach the swimmer, he has to travel a
distance 126 m from the boat. At the same time, the girl spots a man riding a
water craft who is 98 m away from the boat. The man n the water craft is due
east of the swimmer. How far must the man travel to rescue the swimmer? Solution
(3) P and Q are points on sides AB and AC respectively, of triangle ABC. If AP = 3 cm, PB = 6 cm, AQ = 5 cm and QC = 10 cm, show that BC = 3 PQ. Solution
(4) In triangle ABC, AB = AC and BC = 6 cm. D is a point on the side AC such that AD = 5 cm and CD = 4 cm. Show that triangle BCD and triangle ACB are congruent and hence find BD. Solution
(5) The points D and E are on the sides AB and AC of triangle ABC respectively, such that DE and BC are parallel. If AB = 3 AD and the area triangle ABC is 72 cm², then find the area of the quadrilateral DBCE.
(6) The lengths of the three sides of triangle ABC are 6 cm, 4 cm and 9 cm. Triangle PQR ad BC are congruent. One of the lengths of the sides of triangle PQR is 35 cm. What is the greatest perimeter possible for triangle PQR
(7) In the figure, the sides DE and BC are parallel and (AD/B) = 3/5, calculate the value of
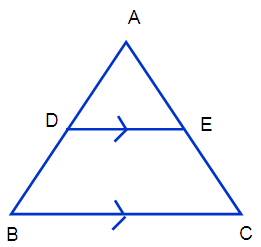
(i) area of triangle ADE/are of triangle ABC
(ii) area of trapezium BCED/area of triangle ABC
(8) The government plans to develop a new industrial zone in an unused portion of land in a city.
The shaded portion of the map shown given below indicates the area of the new industrial zone. Find the area of the new industrial zone.
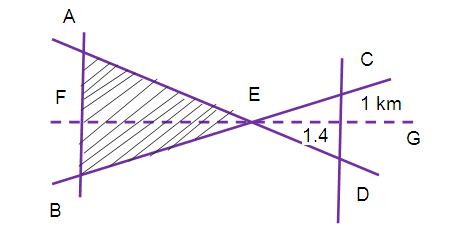
(9) A boy is designing a diamond shaped kite, as shown in the figure where AE = 16 cm, EC = 81 cm. He wants to use a straight cross bar BD. How long should it be?
(10) A student wants to determine the height of flag pole. He placed a small mirror on the ground so that he can see reflection of the top of the flagpole. The distance of the mirror from him is 0.5 m and the distance of the flagpole from the mirror is 3 m .If t he eyes are 1.5 m above the ground level, then find the height of the flagpole (The foot of student, mirror and the foot of flagpole lie along the a straight line) Solution
(11) A roof has a cross section as shown in the diagram
(i) Identify the similar triangles
(ii) Find the height h of the roof. Solution
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Practice Test Using Algebraic Identities
May 11, 21 09:31 PM
Practice Test Using Algebraic Identities
-
Practice Questions in Algebraic Identities
May 10, 21 11:05 AM
Practice Questions in Algebraic Identities
-
Sum of the Angles of a Triangle Worksheet
May 08, 21 10:39 AM
Sum of the Angles of a Triangle Worksheet
