SOLVING WORD PROBLEMS IN SIMILAR TRIANGLES

Problem 1 :

The lengths of the three sides of triangle ABC are 6 cm, 4 cm and 9 cm. Triangle PQR ad BC are congruent. One of the lengths of the sides of triangle PQR is 35 cm. What is the greatest perimeter possible for triangle PQR

Solution :

From the given information let us draw a rough diagram.

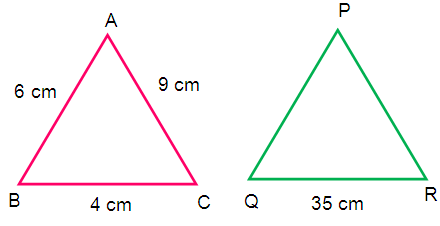
∆ PQR ~ ∆ ABC

PQ/AB = QR/BC = PR/AC = perimeter of ∆ PQR/Perimeter of ∆ BC

Let QR = 35

The corresponding sides must be QR and BC.

Perimeter of ∆ PQR / Perimeter of ∆ ABC is 

=  QR/BC

=  35/4

Perimeter of triangle PQR = (35/4) ⋅ 19

  =  665/4

  =  166.25

So, perimeter of triangle PQR is 166.25 cm².

Problem 2 :

In the figure given below, the sides DE and BC are parallel and (AD/B) = 3/5, calculate the value of

(i)  area of triangle ADE/are of triangle ABC

(ii)  area of trapezium BCED/area of triangle ABC

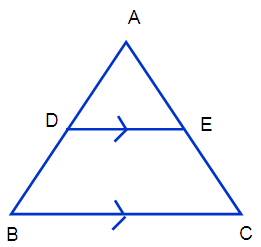
Solution :

In triangle ABC, the sides DE and BC are parallel 

Area of ∆ ADE/ Area of ∆ ABC  =  AD²/AB²

  =  (3k)²/(8k)²

  =  9/64

(ii)  Area of ∆ ADE  =  9 k      

Area of ∆ ADE  =  64 k

Area of trapezium BCDE  =  area of ∆ ABC – area of ∆ ADE

  =  64 k – 9 k

  =  55 k

Area of trapezium BCDE/Area of ∆ ABC  =  55 k/64 k

  =  55/64

Problem 3 :

The government plans to develop a new industrial zone in an unused portion of land in a city.

The shaded portion of the map shown given below indicates the area of the new industrial zone. Find the area of the new industrial zone.

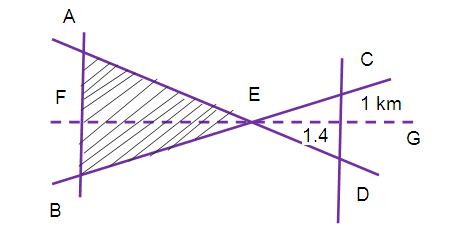
Solution :

By considering the lines AD and BC,the angles

∠AEB  =  ∠DEC (vertically opposite angles)

∠ EAB  =  ∠EDC (alternate angles)      

By using AA similarity criterion ∆ EAB ~ ∆ EDC

(AB/DC)  =  (EF/EG)

EF  =  (AB/DC) x EG

  =  (3/1) x 1.4

  =  4.2 km

Area of new industrial zone = Area of ∆ EAB

  =  (1/2) ⋅ AB ⋅ EF

  =  (1/2) ⋅ 3 ⋅ 4.2

  =  6.3 km²

So, the area of new industrial zone is 6.3 km²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.