SIMILAR TRIANGLES WORD PROBLEMS

Problem 1 :

The government plans to develop a new industrial zone in an unused portion of land in a city.

The shaded portion of the map shown given below indicates the area of the new industrial zone. Find the area of the new industrial zone.

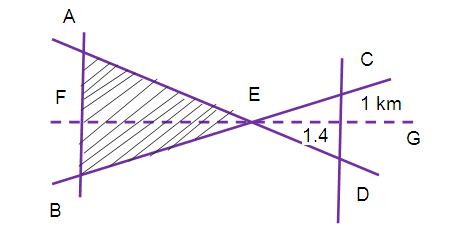
Solution :

By considering the lines AD and BC,the angles

∠AEB  =  ∠DEC (vertically opposite angles)

∠EAB  =  ∠EDC (alternate angles)                 

By using AA similarity criterion ∆ EAB ~ ∆ EDC

(AB/DC)  =  (EF/EG)

EF  =  (AB/DC) ⋅ EG

  =  (3/1) ⋅ 1.4

  =  4.2 km

Area of new industrial zone = Area of ∆ EAB

  =  (1/2) ⋅ AB ⋅ EF

  =  (1/2) x 3 x 4.2

  =  6.3 km²

So the area of new industrial zone is 6.3 km²

Problem 2 :

A boy is designing a diamond shaped kite, as shown in the figure where AE = 16 cm, EC = 81 cm. He wants to use a straight cross bar BD. How long should it be?

Solution :

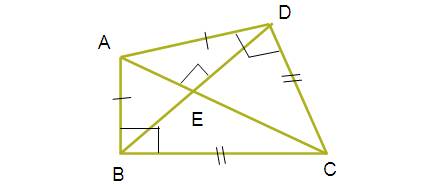
∆ EAD ~ ∆ EDC

So, EA/ED  =  ED/EC

ED²  =  EA ⋅ EC

  =  16 ⋅ 81

  =  √16 ⋅ 81

  =  4 ⋅ 9

  =  36

ABD is the isosceles right triangle and the side AE is perpendicular to the side BD.

BE  =  ED

So,

BD  =  2 ED

 =  2(36)  ==>  72 cm

Problem 3 :

A student wants to determine the height of flag pole. He placed a small mirror on the ground so that he can see reflection of the top of the flagpole. The distance of the mirror from him is 0.5 m and the distance of the flagpole from the mirror is 3 m .If t he eyes are 1.5 m above the ground level, then find the height of the flagpole (The foot of student, mirror and the foot of flagpole lie along the a straight line)

Solution :

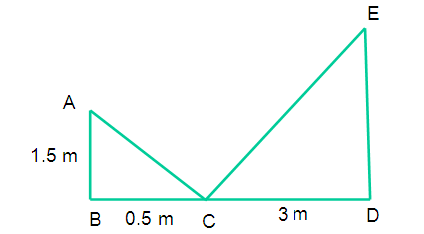
Let “C” be point of reflection

In triangles ABC and EDC

∠ABC  =  ∠EDC  =  90 degree

∠BCA  =  ∠DCE

By using AA criterion ∆ABC  ~  ∆EDC

AB/ED  =  BC/DC

1.5/ED  =  0.5/3

4.5  =  0.5 ED

ED  =  4.5/0.5

  =  9 m

Therefore height of flag pole  =  9 m

Problem 4 :

A roof has a cross section as shown in the diagram

(i) Identify the similar triangles

(ii) Find the height h of the roof.

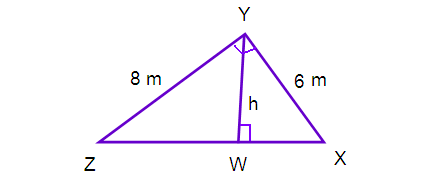
Solution :

Corresponding triangles from the given picture

(i) ∆ WZY ~ ∆ YZX

(ii) ∆ WYX ~ ∆ YZX

(iii) WZY ~ ∆ WYZ

From the (ii)

WY/YZ  =  XY/XZ

h/8  =  6/10

h  =  (6/10) ⋅ 8

h  =  48/10

h  =  4.8 m

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.