PRACTICE PROBLEMS ON FINDING ROOTS OF A COMPLEX NUMBER
Find the cube roots of a complex number
1) 2(cos 2π + i sin 2π)
2) 2(cos π/4 + i sin π/4)
3) 3(cos 4π/3 + i sin 4π/3)
4) 27(cos 11π/6 + i sin 11π/6)
5) -2 + 2i
6) Determine the fourth roots of –8 + 8√3 i . Give answers in rectangular form.
Answers :
|
1) z0 = 3√2(cis (2π/3)) z1 = 3√2(cis (8π/3)) z2 = 3√2(cis (10π/3)) |
2) z0 = 3√2(cis (π/12)) z1 = 3√2(cis (9π/12)) z2 = 3√2(cis (17π/12)) |
|
3) z0 = 3√3(cis (4π/9)) z1 = 3√3(cis (10π/9)) z2 = 3√2[cis (16π/9)) |
4) z0 = 3(cis (11π/18)) z1 = 3(cis (23π/18)) z2 = 3(cos (35π/18)) |
|
5) z0 = 6√8(cis (3π/12)) z1 = 6√8(cos (11π/12)) z2 = 6√8(cos (19π/12)) |
6) z0 = (√3 + i) z1 = (-1 + i√3) z2 = -√3 - i z3 = 1 - i√3 |
Find the nth roots of a complex number
1) 1 + i, n = 4
2) 1 - i, n = 6
3) 2 + 2i, n = 3
4) -2 + 2i, n = 4
Answer Key
|
1) z0 = 8√2(cis (π/16)) z1 = 8√2(cis (9π/16)) z2 = 8√2(cis (17π/16)) z3 = 8√2(cis (25π/16)) |
2) z0 = 12√2(cis (π/24)) z1 = 8√2(cis (7π/24)) z2 = 12√2(cis (5π/8)) z3 = 12√2(cis (23π/24)) z4 = 12√2(cis (31π/24)) z5 = 12√2(cis (39π/24)) |
|
3) z0 = 6√8(cis (π/12)) z1 = 6√8(cis (3π/4)) z2 = 6√8(cis (17π/12)) |
4) z0 = 8√8(cis (3π/16)) z1 = 8√8(cis (11π/16)) z2 = 8√8(cis (19π/16)) z3 = 8√8(cis (27π/16)) |
Find the indicated power of a complex number
1) (cos π/4 + i sin π/4)3
2) [3(cos 3π/2 + i sin 3π/2)]5
3) [2(cos 3π/4 + i sin 3π/4)]3
4) (1 + i)5
5) (1 - √3i)3
6) (-1 - 6i)3
7) (3 – 2i)(5 + 4i) – (3 – 4i)2
8) (1 - 2i)2 - (1 + 2i)2
9) (2 + 3i)2 - (2 - 3i)2
Answer Key
|
1) z3 = -√2/2 + i √2/2 2) z5 = 243i 3) z3 = 4√2 + i 4√2 4) z5 = -4 - 4i 5) z3 = -8 |
6) 107 + 198i 7) 23 + 2i 8) -8i 9) 24i |
1) Find the square root of the following
7 - 24i
2) Find the square root of the following
-15 - 8i
3) Find the square root of the following
-8 - 6i
4) Find the square root of the following
-3 + 4i
5) If [(1 - i)/(1 + i)]100 = a + ib, then find ab.
6) If 1 + i is the root of the equation x2 + ax + b where a and b ∈ then find the value of a + b.
Answer Key
1) Hence the square root of the given complex number are
4 - 3i or (-4 + 3i)
2) Hence the square root of the given complex number are
1 - 4i or (-1 + 4i)
3) Hence the square root of the given complex number are
1 - 3i or (-1 + 3i)
4) Hence the square root of the given complex number are
1 + 2i or (-1 - 2i)
5) ab = 0
6) the value of a + b = 0
Question 1 :
Solve the equation z3 + 27 = 0
Question 2 :
If ω ≠ 1 is a cube root of unity, show that the roots of the equation (z −1)3 + 8 = 0 are −1, 1− 2ω, 1− 2ω2
Question 3 :
Find the value of
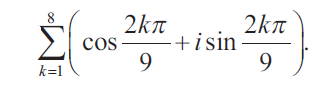
Question 4 :
If ω ≠ 1 is a cube root of unity, show that
(i) (1 − ω + ω2)6 + (1 + ω − ω2)6 = 128.
(ii) (1 − ω)(1 + ω2)(1 + ω4)(1 + ω8).............(1 + ω2^11) = 1
Question 5 :
If z = 2 - 2i, find rotation of z by θ radians in the counter clock wise direction about the origin when
(i) θ = π/3 (ii) θ = 2π/3 (iii) θ = 3π/2
Question 6 :
If
[(1 + i)/(1 - i)]3 - [(1 - i)/(1 + i)]3 = x + iy
then find (x, y).
Answer Key
1) 3 cis (π/3), -3, 3 cis (5π/3)
2) Proved
3) 1
4) proved
5) i) 2√2 (cos (π/12) + i sin (π/12))
ii) 2√2 (cos (5π/12) + i sin (5π/12))
iii) 2√2 (cos (5π/4) + i sin (5π/4))
6)