POSTULATES AND THEOREMS

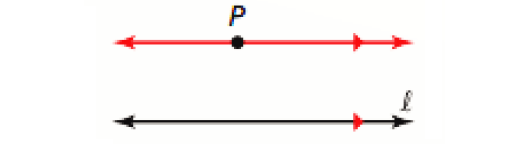
Parallel Postulate :

If there is a line and a point not on the line, then there is exactly one line through the point parallel to the given line.

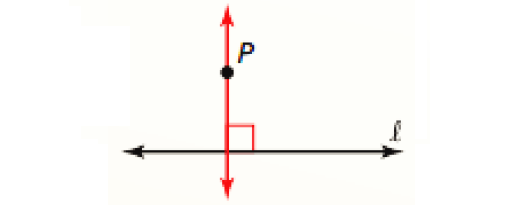
Perpendicular Postulate :

If there is a line and a point not on the line, then there is exactly one line through the point perpendicular to the given line.

Corresponding Angles Theorem :

If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent.

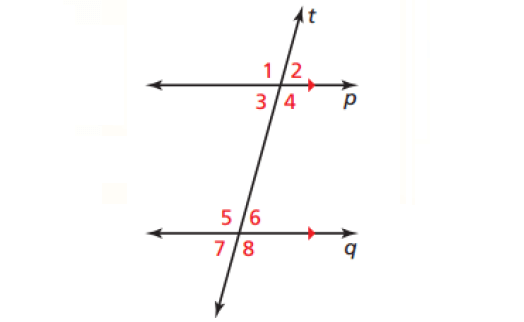
In the above diagram,

m∠1 ≅ m∠5

m∠2 ≅ m∠6

m∠3 ≅ m∠7

m∠4 ≅ m∠8

Alternate Interior Angles Theorem :

If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent.

In the above diagram,

m∠3 ≅ m∠6

m∠4 ≅ m∠5

Alternate Exterior Angles Theorem :

If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent.

In the above diagram,

m∠1 ≅ m∠8

m∠2 ≅ m∠7

Consecutive Interior Angles Theorem :

If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are supplementary.

In the above diagram,

m∠3 + m∠5 = 180°

m∠4 + m∠6 = 180°

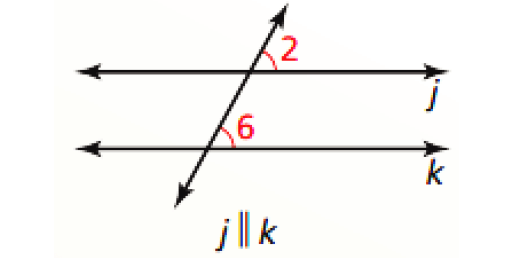
Corresponding Angles Converse :

If two lines are cut by a transversal so the corresponding angles are congruent, then the lines are parallel.

Alternate Interior Angles Converse :

If two lines are cut by a transversal so the alternate interior angles are congruent, then the lines are parallel.

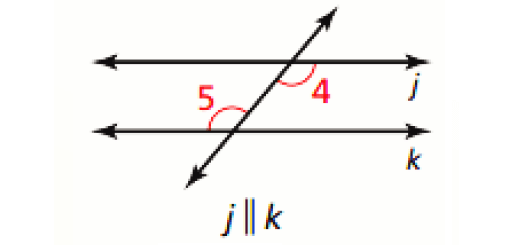
Alternate Exterior Angles Converse :

If two lines are cut by a transversal so the alternate exterior angles are congruent, then the lines are parallel.

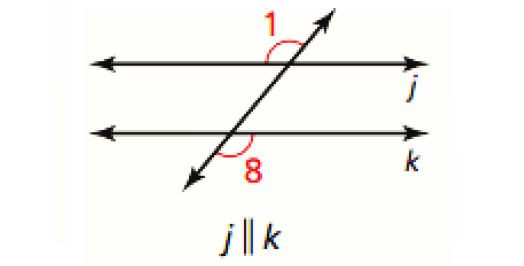
Consecutive Interior Angles Converse :

If two lines are cut by a transversal so the consecutive interior angles are supplementary, then the lines are parallel.

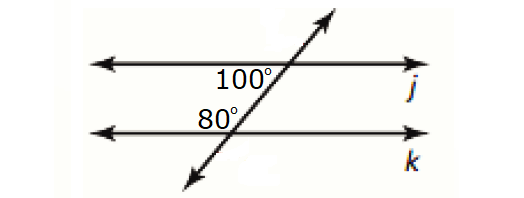
In the diagram above, the lines j and k are parallel.

j ∥ k

Transitive Property of Parallel Lines :

If two lines are parallel to the same line, then they are parallel to each other.

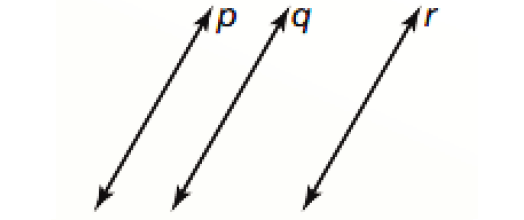
In the diagram above, if p ∥ q and q ∥ r, then p ∥ r.

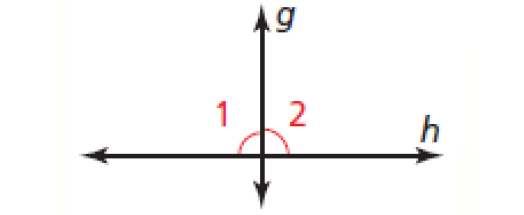
Linear Pair Perpendicular Theorem :

If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular.

Perpendicular Transversal Theorem :

In a plane, if a transversal is perpendicular to one of two parallel lines, then it is perpendicular to the other line.

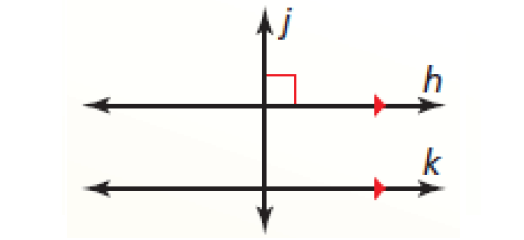
In the diagram above, line j is perpendicular to line k.

j ⊥ k

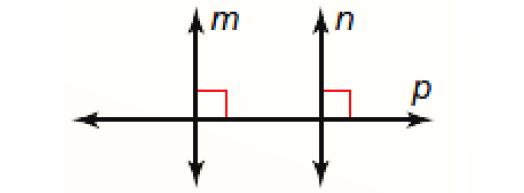
Lines Perpendicular to a Transversal Theorem :

In a plane, if two lines are perpendicular to the same line, then they are parallel to each other.

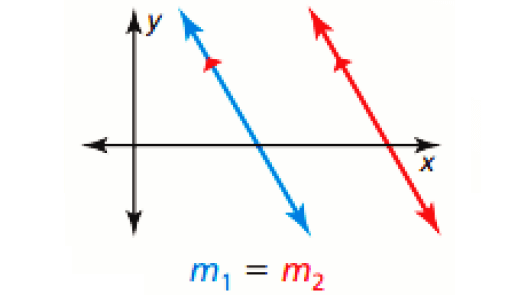
Slopes of Parallel Lines :

In a coordinate plane, two distinct nonvertical lines are parallel if and only if they have the same slope. Any two vertical lines are parallel.

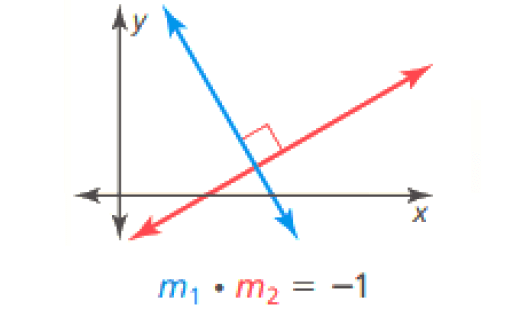
Slopes of Perpendicular Lines :

In a coordinate plane, two nonvertical lines are perpendicular if and only if the product of their slopes is -1. Horizontal lines are perpendicular to vertical lines.

Note :

A postulate is a statement that is assumed true without proof. A theorem is a true statement that can be proven. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.