OPERATIONS WITH RADICALS WORKSHEET

Simplify the following

(1)  (3√2)²

(2)  - 2√3 × 4√3

(3)  3√2 - √8

(4)  2√3 × 3√5

(5)  (2√5)²

(6)  5√2 - 7√2

(7)  (√3)⁴

(8)   √3 × √5 × √15

(9)  Write √48 in simplest radical form.

(10)  Write √75 in simplest radical form.

(11)  What is the set of all solutions to the equation

√(x + 18) = −2x?

(A) {−2, −6}     (B) {−2}    (C) {3}

(D) There are no solutions to the given equation.

(12)  

³√8x³

If x < 0, which of the following is equivalent to the expression above ?

(A) -8x     (B) -2x   (C) 2x    (D) 2x³

(13)  

√x = x - 2

What is the greatest value of x that satisfies the above equation ?

(14)  

If a = 3√7/4 and 4a = √3b, what is the value of b ?

(A) 4/3     (B) 7   (C) 21    (D) 63

(15)  Simplify the radical expression 6/√3 ?

(16)  2√45 - 2√5

(17)  -3√5 - √6 - √5

(18)  √2(√6 - √10)

(19)  √49a⁸x¹²

(20)  √5xy √40x³y

(21)  ³√162x⁵/³√3x²

Solution

Expand and simplify 

(11)  Write √1/7 in the form k√7

(12)  Find x, y ∈ Q such that

(3+x√5) (√5–y)  =  -13+5√5

(13)  Find p, q  ∈ Q such that

(p+3√7) (5+q√7)  =  9√7-53

(14)  Solve for m, √(m - 1) + 5 = m - 2

Solution

Dividing radicals

Solution

Problem 1 : 

Simplify the radical expression : 

√169 + √121

Solution

Problem 2 :

Simplify the radical expression : 

√20 + √320

Solution

Problem 3 : 

Simplify the radical expression : 

√117 - √52

Solution

Problem 4 :

Simplify the radical expression : 

√243 - 5√12 + √27

Solution

Problem 5 :

Simplify the radical expression : 

-√147 - √243(8√117) 2√52)

Solution

Problem 6 :

Simplify the radical expression : 

(√13)(√26)

Solution

Problem 7 :

Simplify the radical expression : 

(3√14)(√35)

Solution

Problem 8 :

Simplify the radical expression : 

(8√117) ÷ (2√52)

Solution

Problem 9 :

Simplify the radical expression : 

(8√3)²

Solution

Problem 10 :

Simplify the radical expression : 

(√2)³ + √8

Solution

Problem 11 :

Simplify the radical expression : 

⁴√(x⁴/16)

Solution

Problem 12 :

Simplify the radical expression : 

³√(125p⁶q³)

Solution

Problem 13 :

If √(0.9 ⋅ 0.09 ⋅ x) = 0.9 ⋅ 0.9√3, then the value of x/3 is :

Solution

Problem 14 :

Find the value of (√1521/11) ⋅ (11/√196)

Solution

Problem 15 :

Find the value of [ √(7√7√7√7) ]

Solution

Problem 16 :

9 √x = √12 + √147, then x is

Solution

Problem 17 :

Find the value of √2304 + √23.04 + √0.2304

Solution

Expand and simplify :

1)  √2 (√5+√2)           Solution

2)  √3 (1-√3)          Solution

3)  √11 (2√11-1)       Solution

4)  2√3 (√3-√5)       Solution

5)  (1+√2) (2+√2)       Solution

6)  (√3+2) (√3-1)       Solution

7) (√5+2) (√5-3)       Solution

8) (2√2+√3) (2√2-√3)       Solution

9)  (2+√3) (2+√3)       Solution

10)  (4-√2) (3+√2)       Solution

11)  (√7-√3) (√7+√3)       Solution

12)  (4-√2) (3-√2)       Solution

13)  

The distance d (in miles) that you can see to the horizon with your eye level h feet above the water is given by

d = √3h/2

How far can you see when your eye level is 5 feet above the water?

Solution

14)  The ratio of the length to the width of a golden rectangle is ( 1 + √5 ) : 2. The dimensions of the face of the Parthenon in Greece form a golden rectangle. What is the height h of the Parthenon?

Solution

15)  The electric current I (in amperes) an appliance uses is given by the formula

I = √(P/R)

where P is the power (in watts and R is the resistance (in ohms). Find the current and appliance uses when the power is 147 watts and the resistance is 5 ohms.

Solution

16)  Find the area of the rectangle given below.

Solution

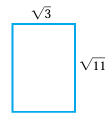
17)  Find the area of the rectangle given below.

Solution

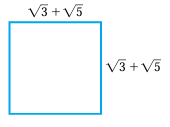
18)  The period of the pendulum is the time required for it to make one complete swing back and forth. The formula of the period P of the pendulum is

P = 2π √(l/32)

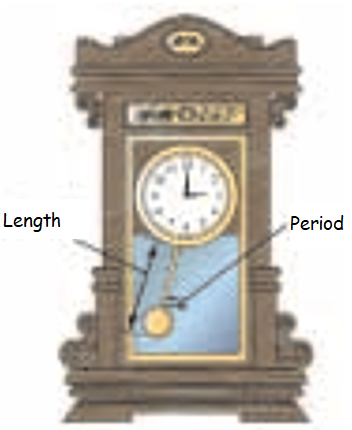
where l is the length of pendulum in feet. If a pendulum in a clock tower is 8 feet long find the period. Use 3.14 for π.

Solution

©All rights reserved. onlinemath4all.com