DIVIDING RADICALS TERMS

When we divide two radical terms, we use the rules given below :

Whenever we have two or more radical terms which are dividing with same index, then we can put only one radical and divide the terms inside the radical. 

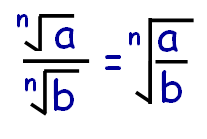
Example 1 :

√5/√20

Solution :

By using radicals property,

We get,

=  √(5/20)

=  √(1/4)

=  √(1/2) ⋅ (1/2)

So, the answer is 1/2

Example 2 :

√27/√3

Solution :

By using radicals property,

We get,

=  √(27/3)

=  √(9/1)

=  √9

=  √(3 . 3)

=  3

So, the answer is 3

Example 3 :

√18/√3

Solution :

By using radicals property,

We get,

=  √(18/3)

=  √(6/1)

=  √6

So, the answer is √6

Example 4 :

√3/√30

Solution :

By using radicals property,

We get,

=  √(3/30)

=  √(1/10)

So, the answer is √(1/10)

Example 5 :

2√6/√24

Solution :

By using radicals property,

We get,

=  2√(6/24)

=  2√(1/4)

=  2√(1/2) . (1/2)

=  2(1/2)

=  1

So, the answer is 1.

Example 6 :

5√75/√3

Solution :

=  5√(75/3)

By simplify, we get

=  2√(25/1)

=  2√(5 . 5)

=  2 × 5

=  10

So, the answer is 10.

Example 7 :

√150 - √54

Solution :

= √150 - √54

Decomposing 150, 150 = 3 x 2 x 5 x 5

Decomposing 54, 54 = 3 x 2 x 3 x 3

= √(3 x 2 x 5 x 5) - √(3 x 2 x 3 x 3)

= 5√6 - 3√6

= 2√6

Example 8 :

21/√7

Solution :

= 21/√7

To rationalize the denominator, we have to multiply by √7 on both numerator and denominator.

= (21/√7) ⋅ (√7/√7)

= 21√7 / (√7⋅√7)

= 21√7 / 7

= 3√7

Example 9 :

(√50 + √18)/√8

Solution :

= (√50 + √18)/√8

= [(√(2⋅5⋅5) + √(3⋅3⋅2)]/2√2

= [5√2 + 3√2]/2√2

= 8√2/2√2

= (8/2)

= 4

Example 10 :

A rectangle has area 12 cm² and length 2 + √7 cm. Find its width in the form of a + b √7, where a and be are integers.

Solution :

Length of the rectangle = 2 + √7 cm

Width of the rectangle = a + b √7

Area of the rectangle = 12 cm²

Length x width = 12

(2 + √7) (a + b√7) = 12

a + b√7 = 12/(2 + √7)

a + b√7 = [12/(2 + √7)] [(2 - √7)/(2 - √7)]

= 12(2 - √7) / (2 + √7) (2 - √7)

= 12(2 - √7)/(2² - √7²)

= 12(2 - √7)/(4 - 7)

= 12(2 - √7)/3

= 4(2 - √7)

Distributing 4, we get

= 8 - 4√7

Comparing with a + b√7

a = 8 and b = -4

Example 11 :

Write the following expression in the form of k √3, where k is an integer.

90/√3 - √6 x √8 - (2√3)³

Solution :

= 90/√3 - √6 x √8 - (2√3)³

= (90/√3) ⋅ (√3/√3) - √(6 x 8) - 8(√3)³

= (90√3/3) - √(2 ⋅ 3 ⋅ 2 ⋅ 2 ⋅ 2) - 8(3)√3

= 30√3 - 4√3 - 24√3

= 30√3 - 28√3

= 2√3

Comparing with k√3, we get the value of k as 2.

Example 12 :

(√7 + 1) / (√7 - 2)

Solution :

= (√7 + 1) / (√7 - 2)

Conjugate of the denominator is (√7 + 2)

= [(√7 + 1) / (√7 - 2)] [(√7 + 2)/(√7 + 2)]

= (√7 + 1)(√7 + 2) / (√7 - 2) (√7 + 2)

= (√7² + 2√7 + √7 + 2) / (√7² - 2²)

= (7 + 3√7 + 2) / (7 - 4)

= (9 + 3√7) / 3

Factoring 3 from the numerator, we get

= 3(3 + √7) / 3

= 3 + √7

Example 13 :

The area of the triangle is (5 + √3) cm² . Given the base of the triangle is √3 cm, find in exact simplified surd form the height of the triangle.

Solution :

Area of the triangle = (5 + √3) cm²

Base = √3

Let h be the height of the triangle

(1/2) x base x height = (5 + √3)

(1/2) x √3 x height = (5 + √3)

height = (5 + √3) ⋅ (2/√3)

= (10 + 2√3)/√3

Rationalizing the denominator, we get

= [(10 + 2√3)/√3] [√3/√3]

= [√3(10 + 2√3)/√3√3]

= [√3(10 + 2√3)/3

= (10√3 + 6)/3

So, the height of the triangle is (10√3 + 6)/3 cm.

Example 14 :

Express (√12 + 2)/(√12 - 2) in the form a + b √3, where a and b are integers.

Solution :

= (√12 + 2)/(√12 - 2)

= [(√12 + 2)/(√12 - 2)][(√12 + 2)/(√12 + 2)]

= (√12 + 2)²/(√12 - 2)(√12 + 2)

= (√12² + 4√12 + 2²)/(√12² - 2²)

= (12 + 4√12 + 4)/(12-4)

= (16 + 4√12)/8

= (4 + √12)/2

Example 15 :

Express (√8 + √18) in the form n√2, where n is an integer.

Solution :

= (√8 + √18)

= √(2 ⋅ 2 ⋅ 2) + √(3 ⋅ 3 ⋅2)

= 2√2 + 3√2

= 5√2

Example 16 :

Solve the equation,

x √20 = 7√5 - √45

Solution :

x √20 = 7√5 - √45

Decomposing the numbers inside the square root.

x √(2⋅2⋅5) = 7√5 - √(3⋅3⋅5)

2x√5 = 7√5 - 3√5

2x√5 = 2√5

x = 1

So, the value of x is 1.

Example 16 :

Express (5√3 - 6)/(2√3 + 3) in the form m + n √3, where m and n are integers.

Solution :

= (5√3 - 6)/(2√3 + 3)

= (5√3 - 6)/(2√3 + 3)[(2√3 - 3)/(2√3 - 3)]

=  (5√3 - 6)(2√3 - 3) / (2√3 + 3) (2√3 - 3)

=  (30 - 15√3 - 12√3 + 18) / ((2√3)² - 3²)

=  (48 - 27√3) / (12 - 9)

=  (48 - 27√3) / 3

=  16 - 9√3

Comparing with m + n √3, values of m and n are 16 and -9 respectively.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.