USING DISTRIBUTIVE PROPERTY WITH RADICALS

When we use distributive property, the following operations may be useful.

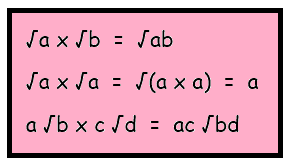
Expand and simplify 

Example 1 :

√2 (√5+√2)

Solution  :

Given, √2 (√5+√2)

By distribution, we get

√2 (√5+√2)  =  √2×√5 + √2×√2

=  √10+2

So, the answer is √10+2.

Example 2 :

√3 (1-√3)

Solution  :

Given, √3 (1-√3)

By distribution, we get

√3 (1-√3)  =  √3×1 - √3×√3

=  √3-3 

Example 3 :

√11 (2√11-1)

Solution  :

Given, √11 (2√11-1)

By distribution, we get

√11 (2√11-1)  =  √11×2√11 - √11×1

=  2×11 - √11

=  22-√11

Example 4 :

2√3 (√3-√5)

Solution  :

Given, 2√3 (√3-√5)

By distribution, we get

2√3 (√3-√5)  =  (2√3×√3)-(2√3×√5)

=  (2x3) - 2√15

=  6-2√15 

Example 5 :

(1+√2) (2+√2)

Solution  :

Given, (1+√2) (2+√2)

By distribution, we get

(1+√2) (2+√2)  =  2+√2+2√2+2

=  4+3√2

Example 6 :

(√3+2) (√3-1)

Solution  :

Given, (√3+2) (√3-1)

By distribution, we get

(√3+2) (√3-1)  =  (√3×√3)-(√3×1)+(2×√3)-(2×1)

=  3-√3+2√3-2

=  1+√3 

Example 7 :

(√5+2) (√5-3)

Solution  :

Given, (√5+2) (√5-3)

By distribution, we get

(√5+2) (√5-3)  =  (√5×√5)-(√5×3)+(2×√5)-(2×3)

=  5-3√5+2√5-6

=  -1-√5

Example 8 :

(2√2+√3) (2√2-√3)

Solution  :

Given, (2√2+√3) (2√2-√3)

By algebraic identity, we get

(2√2+√3) (2√2-√3)  =  (2√2)²-(√3)²

=  4×2 - 3

=  5

Example 9 :

(2+√3) (2+√3)

Solution  :

Given, (2+√3) (2+√3)

By distribution, we get

(2+√3) (2+√3)  =  2×2+(2×√3)+(√3×2)+(√3×√3)

=  4+2√3+2√3+3

=  7+4√3

Example 10 :

(4-√2) (3+√2)

Solution  :

Given, (4-√2) (3+√2)

By distribution, we get

(4-√2) (3+√2)  =  (4×3)+(4×√2)-(√2×3)-(√2×√2)

=  12+4√2-3√2-2

=  10+√2 

Example 11 :

(√7-√3) (√7+√3)

Solution  :

Given, (√7-√3) (√7+√3)

By using algebraic identity

(a+b)(a-b)  =  a²-b²

(√7-√3) (√7+√3)  =  (√7)²-( √3 )²

=  7-3

=  4

Example 12 :

(4-√2) (3-√2)

Solution :

Given, (4-√2) (3-√2)

By distribution, we get

(4-√2) (3-√2)  =  4×3 - (4×√2) - (√2×3) + (√2×√2)

=  12-4√2-3√2+2

=  14-7√2

Example 13 :

The distance d (in miles) that you can see to the horizon with your eye level h feet above the water is given by

d = √3h/2

How far can you see when your eye level is 5 feet above the water?

Solution :

d = √(3h/2)

height = 5 feet

d = √(3(5)/2)

= √15/√2

To rationalize the denominator, we multiply both numerator and denominator by √2.

= (√15/√2) ⋅ (√2/√2)

= √15√2/√2√2

= √30/2

= 5.47/2

= 2.73 feet

So, we can see about 2.73 feet.

Example 14 :

The ratio of the length to the width of a golden rectangle is ( 1 + √5 ) : 2. The dimensions of the face of the Parthenon in Greece form a golden rectangle. What is the height h of the Parthenon?

Solution : 

By comparing the given ratio width with length and width from the picture, we get

(1 + √5) : 2 = 31 : h

(1 + √5) / 2 = 31 / h

h(1 + √5) = 31(2)

h(1 + √5) = 62

h = 62/(1 + √5)

Rationalizing the denominator, we get

h = [62/(1 + √5)] [(1 - √5)/(1 - √5)]

= 62(1 - √5) / (1 + √5)(1 - √5)

= 62 (1 - √5)/(1-5)

= -62 (1 - √5)/4

= -15.5(1 - 2.23)

= -15.5(-1.23)

= 19.065 m

Example 15 :

The electric current I (in amperes) an appliance uses is given by the formula

I = √(P/R)

where P is the power (in watts and R is the resistance (in ohms). Find the current and appliance uses when the power is 147 watts and the resistance is 5 ohms.

Solution :

I = √(P/R)

When P = 147 and R = 5, then I = ?

I = √(147/5)

To rationalize the denominator, we have to multiply both numerator and denominator by √5

I = [√147/√5] [√5/√5]

= √(147x5) / 5

= √735 / 5

= 27.11/5

= 5.42 amperes

Example 16 :

Find the area of the rectangle given below.

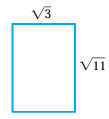
Solution :

Length of the rectangle = √11

Width = √3

Area of rectangle = length x width

= √11 x √3

= √(11 x 3)

= √33

Example 16 :

Find the area of the rectangle given below.

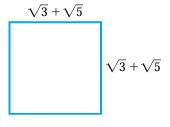
Solution :

Length of the rectangle = √3 + √5

Width = √3 + √5

Area of rectangle = length x width

= (√3 + √5) x (√3 + √5)

= √3√3 + √3(√5) + √5(√3) + √5 √5

= 3 + √(3 x 5) + √(3 x 5) + 5

= 8 + √15 + √15

= 8 + 2√15

Example 17 :

The period of the pendulum is the time required for it to make one complete swing back and forth. The formula of the period P of the pendulum is

P = 2π √(l/32)

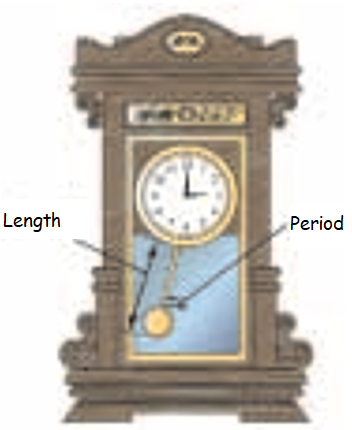
where l is the length of pendulum in feet. If a pendulum in a clock tower is 8 feet long find the period. Use 3.14 for π.

Solution :

P = 2π √(l/32)

l = 8 feet

P = 2π √(8/32)

P = 2π √(1/4)

P = 2x 3.14 x (1/2)

= 3.14 feet

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.