EXPAND AND SIMPLIFY WITH RADICALS

Expand and simplify :

Problem 1 :

2√3(4-√3)

Solution :

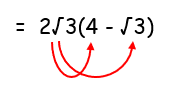
=  (2√3 ⋅ 4) – (2√3 ⋅ √3)

=  8√3 – 6

So, the answer is 8√3–6.

Problem 2 :

- √2(2-√2)

Solution :

-√2(2-√2)  =  - 2√2 + (√2 ⋅ √2)

=  - 2√2 + 2

=  2 - 2√2

So, the answer is 2-2√2.

Problem 3 :

2√3(√3 - 1) - 2√3

Solution :

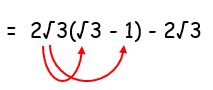
=  (2√3 ⋅ √3) – 2√3 - 2√3

=  6 - 2√3 - 2√3

=  6 - 4√3

So, the answer is 6 - 4√3.

Problem 4 :

(2√2 - 5)(1 - √2)

Solution :

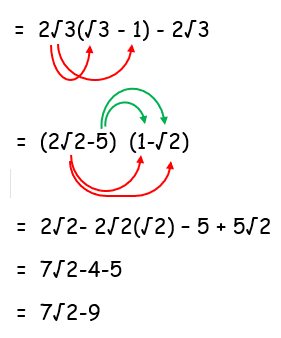
Problem 5 :

(3 + 2√5)(2 - √5)

Solution :

By using distributive property,

We get,

=  (3 + 2√5)(2 - √5)

=  6 - 3√5 + 4√5 – (2⋅5)

=  6-10-3√5+4√5

=  - 4+√5

=  √5-4

So, the answer is √5-4.

Problem 6 :

(4 - √2)(3 + 2√2)

Solution :

By using distributive property,

We get,

=  (4 - √2)(3 + 2√2)

=  (4 ⋅ 3) + (4 ⋅ 2√2) - (√2 ⋅ 3) – (√2 ⋅ 2√2)

=  12 + 8√2 - 3√2 – (2 ⋅ 2)

=  12 + 8√2 - 3√2 – 4

=  8 + 5√2

So, the answer is 8 + 5√2.

Problem 7 :

(3 - √7)²

Solution :

By comparing the given question with the algebraic identity (a-b)², we get

(a-b)²  =  a²-2ab+b²

Here a  =  3 and b  =  √7

=  3² – (2 ⋅ 3 ⋅ √7) + (√7)²

=  9-6√7+7

=  16-6√7

So, the answer is 16 - 6√7.

Problem 8  :

- (2 - √5)²

Solution :

By comparing the given question with the algebraic identity (a-b)², we get

(a-b)²  =  a²-2ab+b²

=  - (2 - √5)²

=  - [2² – (2⋅ 2⋅ √5) + (√5)²]

=  - [4-4√5+5]

=  - [9-4√5]

=  - 9+4√5

=  4√5-9

So, the answer is 4√5-9.

Problem 9 :

(2 - √3)(2 + √3)

Solution :

By comparing the given question with algebraic identity a²-b², we get

a²-b²  =  (a+b)(a-b)

Here a = 2 and b = √3

=  (2 - √3)(2 + √3)

 =  (2)² – (√3)²

=  1

So, the answer is 1.

Problem 10 :

(5 - √3)(5 + √3)

Solution :

By using algebraic identity,

We get,

=  (5 - √3)(5 + √3)

 =  (5)² – (√3)²

=  22

So, the answer is 22.

Problem 11 :

Write √1/7 in the form k√7

Solution :

Given, √1/7

=  1/√7 ⋅ (√7/√7)

=  √7/7

=  (1/7) √7

The value of k is 1/7.

Problem 12 :

Find x, y ∈ Q such that (3+x√5) (√5–y)  =  - 13+5√5

Solution :

(3 + x√5) (√5 – y)  =  - 13 + 5√5

3√5 – 3y + 5x - xy√5  =  - 13 + 5√5

5x – 3y + √5(3 - xy)  =  - 13 + 5√5

Equating corresponding terms, we get

5x – 3y  =  - 13 -----(1)

(3 – xy)  =  5

- xy  =  2

y  =  - 2/x -----(2)

By applying y  =  - 2/x in (1),

We get,

5x – 3y  =  - 13

5x – 3(- 2/x)  =  - 13

5x + (6/x)  =  - 13

5x² + 6  =  - 13x

5x² + 13x + 6  =  0

By factorization, we get

5x² + 10x + 3x + 6  =  0

5x(x+2) + 3(x+2)  =  0

(5x+3) (x+2)  =  0

By applying x  =  - 2 in (2),

We get,

y  =  -2/x

y  =  1

So, the value of x  =  - 2 and y  =  1

Problem 13  :

Find p, q  ∈ Q such that (p + 3√7) (5 + q√7)  =  9√7 - 53

Solution :

(p + 3√7) (5 + q√7)  =  9√7 - 53

5p + pq√7 + 15√7 + (3q . 7)  =  9√7 – 53    

(5p+21q) + √7(pq+15)   =  9√7 - 53

By combining like same terms, we get

5p + 21q  =  - 53 -----(1)

pq + 15  =  9

pq  =  - 6

q  =  - 6/p -----(2)

By applying q  =  - 6/p in (1),

We get,

5p + 21q  =  - 53

5p + 21(- 6/p)  =  - 53

5p - (126/p)  =  - 53

5p² - 126  =  - 53p

5p² + 53p - 126  =  0

By factorization, we get

5p² – 10p + 63p - 126  =  0

5p(p - 2) + 63(p - 2)  =  0

(5p + 63) (p - 2)  =  0

Problem 14  :

Solve for m, √(m - 1) + 5 = m - 2

Solution :

√(m - 1) + 5 = m - 2

Subtracting 5 on both sides

√(m - 1) = m - 2 - 5

√(m - 1) = m - 7

Squaring on both sides

(m - 1) = (m - 7)²

m - 1 = m² - 14m + 49

m² - 14m - m + 49 + 1 = 0

m² - 15m + 50 = 0

(m - 10)(m - 5) = 0

Solving for m, we get 

m = 10 and m = 5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.