SOLVING LINEAR EQUATIONS IN TWO VARIABLES USING GRAPHICAL METHOD

Solve the following systems of linear equations using graphical method :

Example 1 :

y = 4x + 3

y = -x - 2

Solution :

y = 4x + 3 :

The given equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.

When x = -1,

y = 4(-1) + 3

= -4 + 3

= -1

(-1, -1)

When x = 0,

y = 4(0) + 3

= 0 + 3

= 3

(0, 3)

Plot the points (-1, -1), and (0, 3) on a xy-plane and connect them.

y = -x - 2 :

The given equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.

When x = -1,

y = -(-1) - 2

= 1 - 2

= -1

(-1, -1)

When x = 0,

y = -0 - 2

= -2

(0, -2)

Plot the points (-1, -1), and (0, -2) on a xy-plane and connect them.

Graph :

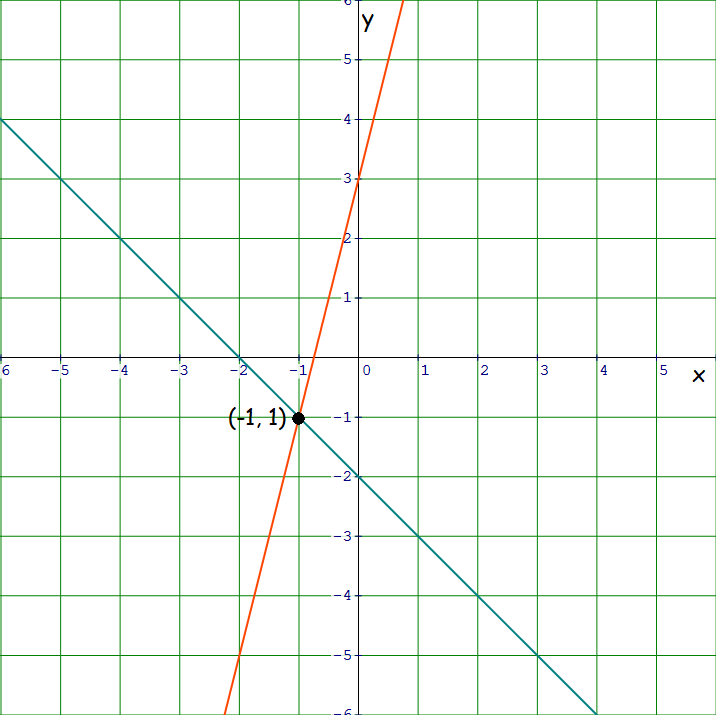
In the graph above, the two lines intersect at (-1, -1).

So, 

x = -1 and y = -1

Example 2 :

5x + 3y - 9 = 0

x - 3y - 9 = 0

Solution :

5x + 3y - 9 = 0 :

The given equation is not in slope-intercept form. Write the given equation is in slope intercept form.

5x + 3y - 9 = 0

Subtract 5x from both sides.

3y - 9 = -5x

Add 9 to both sides.

3y = -5x + 9

Divide both sides by 3.

y = -5x/3 + 3

Now the equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.

In the equation y = -5x/3 + 3, the denominator for the x-term is 3. So, substitute values for x which are the multiples of 3.

When you substitute values for x which are multiples of 3, the values of y will be integers and it will make our graphing process easier.

When x = 0,

y = -5(0)/3 + 3

= 0 + 3

= 3

(0, 3)

When x = 3,

y = -5(3)/3 + 3

= -5 + 3

= -2

(3, -2)

Plot the points (0, 3), and (3, -2) on a xy-plane and connect them.

x - 3y - 9 = 0 :

The given equation is not in slope-intercept form. Write the given equation is in slope intercept form.

x - 3y - 9 = 0

Add 3y to both sides.

x - 9 = 3y

Divide both sides by 3.

x/3 - 3 = y

or

y = x/3 - 3

Now the equation is in slope-intercept form. Substitute some random values for x and find their corresponding values of y.

In the equation y = x/3 - 3, the denominator for the x-term is 3. So, substitute values for x which are the multiples of 3.

When you substitute values for x which are multiples of 3, the values of y will be integers and it will make our graphing process easier.

When x = 0,

y = 0 - 3

= -3

(0, -3)

When x = 3,

y = 3/3 - 3

= 1 - 3

= -2

(3, -2)

Plot the points (0, -3), and (3, -2) on a xy-plane and connect them.

Graph :

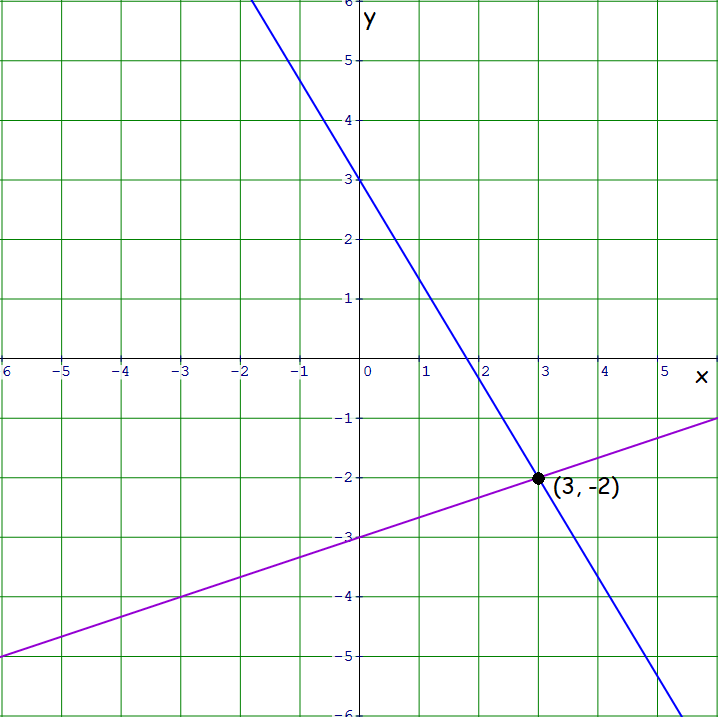
In the graph above, the two lines intersect at (3, -2).

So, 

x = 3 and y = -2

Example 3 :

A roofing contractor buys 30 bundles of shingles and 4 rolls of roofing paper for $1040. In a second purchase (at the same prices), the contractor buys 8 bundles of shingles for $256. Find the price per bundle of shingles and the price per roll of roofing paper

Solution :

Let x be the price of one bundle of shingles

Let y be the price of roll of roofing paper

30x + 4y = 1040

8x = 256

x = 256/8

x = 32

Applying the value of x, we get

30(32) + 4y = 1040

960 + 4y = 1040

4y = 1040 - 960

4y = 80

y = 80/4

y = 20

Cost of one bundle of shingles is $32 and cost of one bundle of roofing paper is $20.

Example 4 :

Describe and correct the error in solving the system of linear equations.

Solution :

The given equations are x - 3y = 6 and 2x - 3y = 3.

By solving these equations using substitution method, we get

x = 6 + 3y

x = 3y + 6

Applying the value of y in 2x - 3y = 3

2(3y + 6) - 3y = 3

6y + 12 - 3y = 3

3y + 12 = 3

3y = 3 - 12

3y = -9

y = -9/3

y = -3

Applying the value of y in x = 3y + 6

x = 3(-3) + 6

x = -9 + 6

x = -3

So, the solution is (-3, -3)

By observing the graph, the point of intersection is (3, -1).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.