MULTIPLICATION OF POLYNOMIALS

Procedure of Multiplying Two Polynomials

We will multiply two or more polynomials in the following order.

(1) Symbol

(2) Number

(3) Variable

Let us see how it works

Multiply (5x²) and (-2x³)

  =  (5x²) (-2x³)

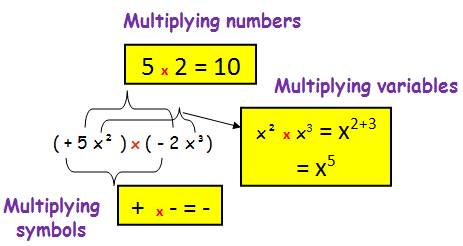
=  10 x⁵

More Examples of Multiplication of Polynomials

Problem 1 :

Multiply (-6x) and (-4x³)

Solution :

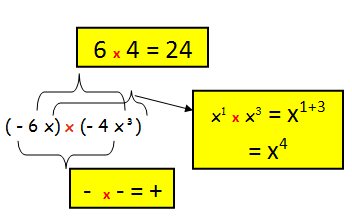
  =  (-6x) x (-4x³)

  =   24 x⁴

Problem 2 :

Multiply (2a-1) and  (8a-5)

Solution :

  =  (2a-1) (8a-5)

To multiply these binomials we have to distribute 2a with (8a-5) and distribute -1 with (8a-5)

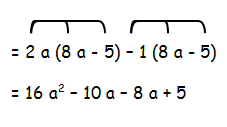
When we combine the like terms,we get

  =  16a²-18a+5

We can do the the same problem in the following flow chart method also.

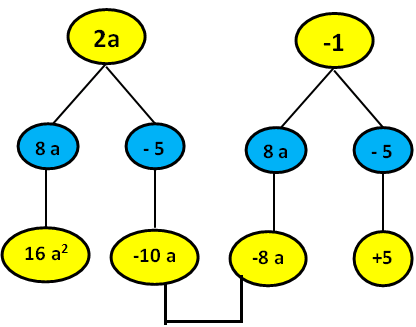
When we combine the like terms,we get

  =  16a²-18a+5

Problem 3 :

Multiply (2a²+5a-1) (8a²-3a+5)

Solution :

  =  (2a²+5a-1) (8a²-3a+5)

To multiply these trinomials, we have to distribute 2 a² with  (8a²-3a+5), distribute 5a with  (8a²-3a+5) and -1 with  (8 a² - 3 a + 5).

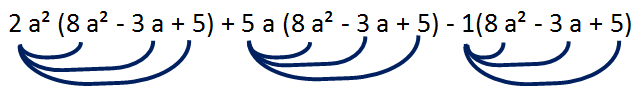
  =  16a⁴-6a³+10a²+40a³-15a²+25a-8a²+3a-5

Now we have to combine the like terms

  =  16a⁴-6a³+40a³+10a²-15a²-8a²+25a+3a-5

  =  16a⁴ + 34 a³ -13 a²+ 28 a - 5

Problem 4 :

Multiply (2x²+5)  and (3y²-4y+7)

Solution :

  =  (2x²+5) (3y²-4y+7)

To multiply these binomial and trinomial we have to distribute 2x² with  (3y²-4y+7) and distribute 5 with  (3y²-4y+7).

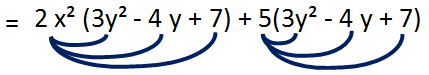
  =  6x²y²-8x²y+14x²+15y²-40y+35

now we have to combine the like terms

=  -2x²y+14x²+15y²-40y+35

Problem 5 :

Multiply (3x+8)  and (4y-7)

Solution :

  =  (3x+8)(4y-7)

To multiply these binomials we have to distribute 3x with  (4y-7) and distribute 8 with (4y-7)

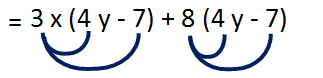
  =  12xy-21x+32y-56

Since there is no like terms. So we cannot simplify this.

Related Pages

• Adding algebraic equation
• Subtracting algebraic equation
• Multiplication of algebraic equations
• Dividing algebraic equation
• Adding algebraic equation Worksheet
• Subtracting algebraic equation Worksheet
• Factoring algebraic equation
• Factoring a Quadratic-Equation
• Factoring Worksheets
• Framing Quadratic Equation From Roots
• Framing Quadratic-Equation Worksheet
• Relationship Between Coefficients and roots
• Roots of Cubic equation
• Roots of Polynomial of Degree4
• Roots of Polynomial of Degree5

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.