DIVISION OF POLYNOMIALS
Let us consider the numbers 13 and 5. When 13 is divided by 5 what is the quotient and remainder?
Yes, of course, the quotient is 2 and the remainder is 3. We write 13 = (5x2) + 3 Let us try.
Dividend = (Divisor x Quotient) + Remainder
From the above examples, we observe that the remainder is less than the divisor.
Division Algorithm for Polynomials
Let p(x) and g(x) be two polynomials such that
degree of p(x) ≥ degree of g(x)
and g(x) ≠ 0. Then there exists unique polynomials q(x) and r(x) such that
p(x) = g(x) ⋅ q(x) + r(x)
where r(x) = 0 or degree of r(x) < degree of g(x).
The polynomial p(x) is the Dividend, g(x) is the Divisor, q(x) is the Quotient and r(x) is the Remainder. Now (1) can be written as
Dividend = (Divisor x Quotient ) + Remainder
If r(x) is zero, then we say p(x) is a multiple of g(x). In other words, g(x) divides p(x).
If it looks complicated, don’t worry! it is important to know how to divide polynomials, and that comes easily with practice. The examples below will help you.
Example 1 :
Dividie (x3 - 4x2 + 6x) by x, where x ≠ 0.
Solution :
Example 2 :
Find the quotient and the remainder when
(5x2 - 7x + 2) ÷ (x - 1)
Solution :
We can use polynomial long division to get the quotient amd remainder when (5x2 - 7x + 2) is divided by (x - 1).
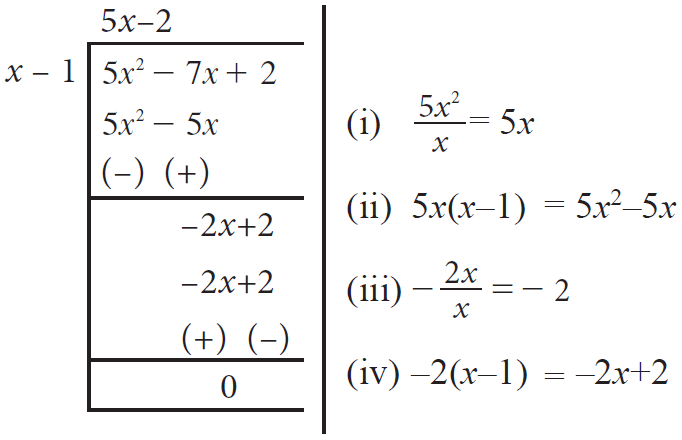
Quotient = 5x - 2
Remainder = 0
Video Lesson
Examples 3-4 : Find quotient and the remainder when f(x) is divided by g(x).
Example 3 :
f(x) = 8x3 - 6x2 + 15x - 7, g(x) = 2x + 1
Solution :
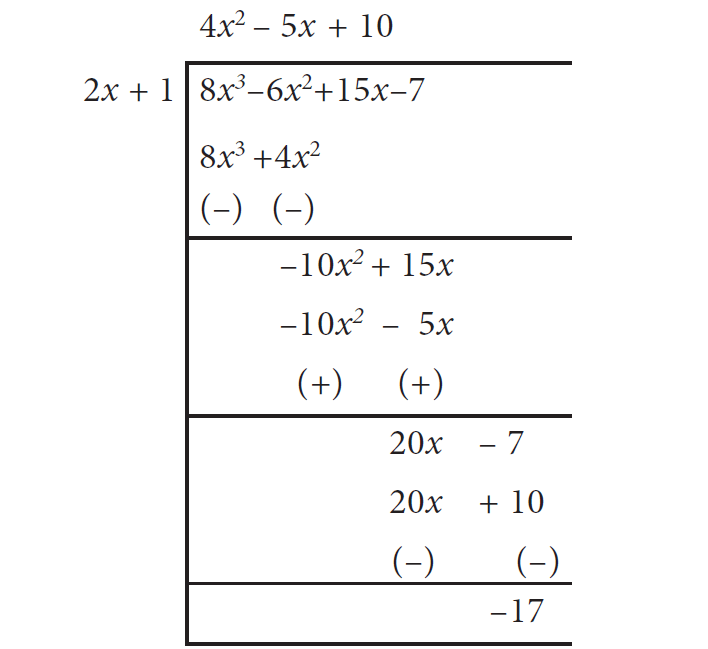
Quotient = 4x2 - 5x + 10
Remainder = -17
Example 4 :
f(x) = x4 - 3x3 + 5x2 - 7, g(x) = x2 + x + 1
Solution :
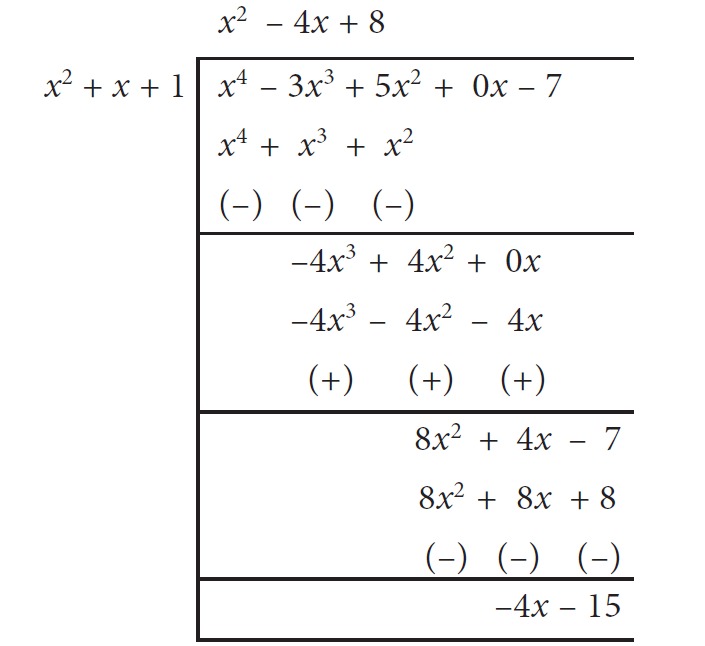
Quotient = x2 - 4x + 8
Remainder = -4x - 15
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Problems on Rates
May 02, 24 02:57 AM
SAT Math Problems on Rates -
Trigonometry Cofunction Identities
Apr 30, 24 09:01 PM
Trigonometry Cofunction Identities -
Worksheet on Unit Rates
Apr 30, 24 08:50 PM
Worksheet on Unit Rates
