HOW TO SOLVE RATIONAL INEQUALITIES

Solve for  x :

Example 1 :

(x + 2)/(x – 3) < 0

Solution :

Let f(x)  =  (x + 2)/(x – 3)

f(x) < 0

(x + 2)/(x – 3) < 0

By equating the numerator and denominator to zero, we get

x + 2  =  0, x – 3  =  0

x  =  -2 and x  =  3 (critical numbers)

The critical numbers are dividing the number line into three intervals.

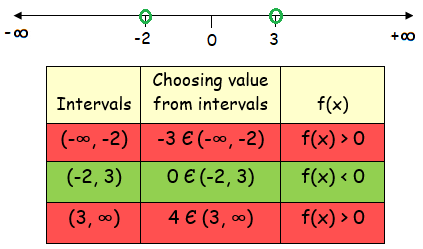
From the table, the possible values of x are

-2 < x < 3

By writing it as interval notation, we get

(-2, 3)

So, the required solution is -2 < x < 3

Example 2  :

(x + 3)/(2 – x) < 0

Solution  :

Let f(x)  =  (x + 3)/(2 – x)

f(x) < 0

(x + 3)/(2 – x) < 0

By equating the numerator and denominator to zero, we get

x + 3  =  0, 2 – x  =  0

x  =  -3 and x  =  2 (critical numbers)

The critical numbers are dividing the number line into three intervals. 

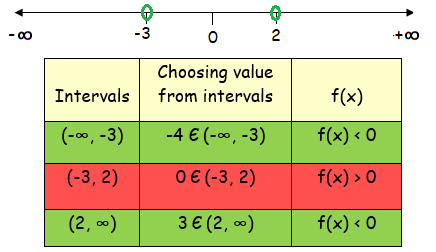
From the table, the possible values of x are

x < -3 or x > 2

By writing it as interval notation, we get

(-∞, -3) u (2, ∞)

So, the required solution is x < -3 or x > 2

Example 3  :

(x - 1)/(x + 3) ≥ -1

Solution  :

Let f(x)  =  (x - 1)/(x + 3)

f(x) ≥ -1

(x - 1)/(x + 3) ≥ -1

Add 1 on both sides, we get

(x - 1)/(x + 3) + 1 ≥ -1 + 1

Taking least common multiple, we get

[(x – 1) + (x + 3)]/(x + 3) ≥ 0

(x - 1 + x + 3)/(x + 3) ≥ 0

(2x + 2)/(x + 3) ≥ 0

By equating the numerator and denominator to zero, we get

2x + 2  =  0, x + 3  =  0

x  =  -1 and x  =  -3 (critical numbers)

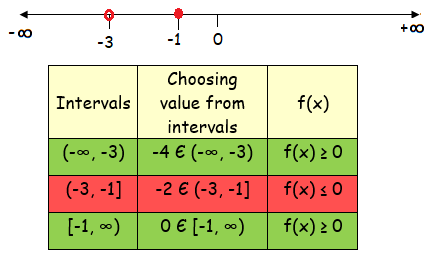
From the table, the possible values of x are

x < -3 or x ≥ -1

By writing it as interval notation, we get

(-∞, -3) u [-1, ∞)

So, the required solution is x < -3 or x ≥ -1

Example 4  :

(x + 2)/(2x - 3) < 1

Solution  :

(x + 2)/(2x - 3) < 1

Subtract 1 on both sides, we get

(x + 2)/(2x - 3) - 1 < 1 – 1

(x + 2)/(2x - 3) - 1 < 0

Taking least common multiple, we get

[(x + 2) + (-2x + 3)]/(2x - 3) < 0

(x + 2 - 2x + 3)/(2x - 3) < 0

-(x - 5)/(2x - 3) < 0

Make a coefficient x as positive, so we have to multiply by -1 through out the equation,

(x - 5)/(2x - 3) > 0

By equating the numerator and denominator to zero, we get

x - 5  =  0, 2x - 3  =  0

x  =  5 and x  =  3/2 (critical numbers)

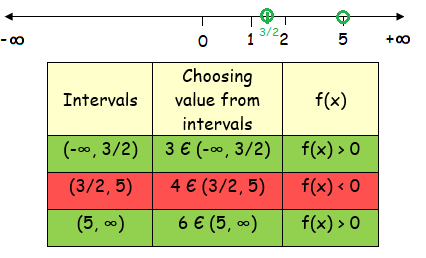
From the table, the possible values of x are

x < 3/2 or x > 5

By writing it as interval notation, we get

(-∞, 3/2) u (5, ∞)

So, the required solution is x < 3/2 or x > 5

Example 5  :

(5 – 2x)/(1 - x) > 4

Solution  :

(5 – 2x)/(1 - x) > 4

Subtract 4 on both sides, we get

(5 – 2x)/(1 - x) - 4 > 4 – 4

(5 – 2x)/(1 - x) - 4 > 0

Taking least common multiple, we get

[(5 – 2x) - 4(1 - x)]/(1 - x) > 0

(5 – 2x - 4 + 4x)/(1 - x) > 0

(2x + 1)/(1 - x) > 0

By equating the numerator and denominator to zero, we get

2x + 1  =  0, 1 - x  =  0

x  =  -1/2 and x  =  1 (critical numbers)

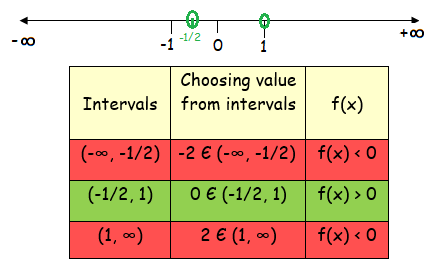
From the table, the possible values of x are

-1/2 < x < 1

By writing it as interval notation, we get

(-1/2, 1)

So, the required solution is -1/2 < x < 1

Example 6  :

4/x ≤ x

Solution  :

4/x ≤ x

Subtract x on both sides, we get

4/x – x ≤ x – x

4/x – x ≤ 0

(4 – x²)/x ≤ 0

By equating the numerator and denominator to zero, we get

4 – x²  =  0, x  =  0      

x  =  ±2, x  =  0

so, x  =  2, x  =  -2 and x  =  0 

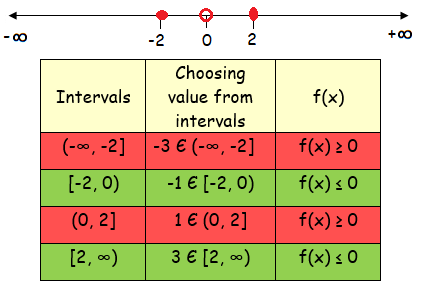
From the table, the possible values of x are

-2 ≤ x < 0 or x ≥ 2

By writing it as interval notation, we get

[-2, 0) u [2, ∞)

So, the required solution is -2 ≤ x < 0 or x ≥ 2

Example 7  :

3/x > 2/(x + 2)

Solution  :

3/x > 2/(x + 2)

Subtract 2/(x + 2) on both sides, we get

3/x – 2/(x + 2)  > 2/(x + 2) - 2/(x + 2)

3/x – 2/(x + 2)  > 0

Taking least common multiple, we get

[3(x + 2) – 2(x)]/x(x + 2) > 0

[3x + 6 – 2x]/x(x + 2) > 0

(x + 6)/x(x + 2) > 0

By equating the numerator and denominator to zero, we get

x + 6  =  0, x(x + 2)  =  0

so, x  =  -6, x  = 0 and x  =  -2

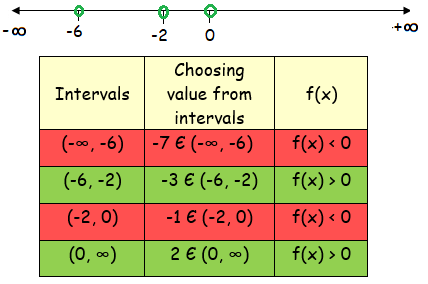
From the table, the possible values of x are

-6 < x < -2 or x > 0

By writing it as interval notation, we get

(-6, -2) u (0, ∞)

So, the required solution is -6 < x < -2 or x > 0

Example 8  :

x/(x + 6) > 3/x

Solution  :

x/(x + 6) > 3/x

Subtract 3/x on both sides, we get

x/(x + 6) – 3/x > 3/x – 3/x

x/(x + 6) – 3/x > 0

Taking least common multiple, we get

[x² – 3(x + 6)]/x(x + 6) > 0

[x² – 3x – 18]/x(x + 6) > 0

By factorization, we get

(x – 6) (x + 3)/x(x + 6) > 0

By equating the numerator and denominator to zero, we get

x - 6  =  0, x + 3  =  0 and x(x + 6)  =  0

So, x  =  6, x  =  -3, x  =  0 and x  =  -6

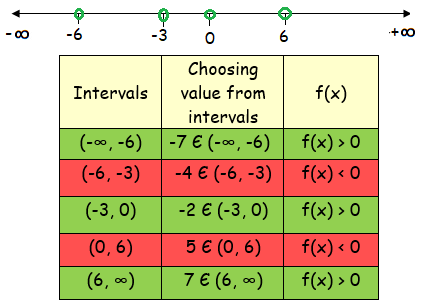
From the table, the possible values of x are

x < -6 or -3 < x < 0 or x > 6

By writing it as interval notation, we get

(-∞, -6) u (-3, 0) u (6, ∞)

So, the required solution is x < -6 or -3 < x < 0 or x > 6

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.