HOW TO FIND ZERO OF A POLYNOMIAL FUNCTION

Find the zeros of the following polynomials

Question 1 :

p(x)  =  4x-1

Solution :

Let p(x)  =  4x-1 

4x-1  =  0

4x  =  1

x  =  1/4

So, 1/4 is the zero of the given polynomial 4x-1.

Question 2 :

p(x)  =  3x+5

Solution :

Let p(x)  =  3x+5

3x+5  =  0

3x  =  -5

x  =  -5/3

So, -5/3 is the zero of the given polynomial 3x+5.

Question 3 :

p(x)  =  2x

Solution :

Let p(x)  =  2x

2x  =  0

x  =  0/2

x  =  0

So, 0 is the zero of the given polynomial 2x.

Question 4 :

p(x)  =  x+9

Solution :

Let p(x)  =  x+9

x+9  =  0

x  =  -9

So, -9 is the zero of the given polynomial x+9.

Verify whether the following are roots of the polynomial equations indicated against them.

Question 1 :

x² - 5x +6  =  0      x  =  2, 3 

Solution :

Given that p(x) =  x² - 5x +6

p(2) =  2² - 5(2) + 6

=  4 -10 + 6

p(2)  =  0

Given that p(x)   =  x² - 5x +6

p(3)  =  3²-5(3)+6

=  9 -15 + 6

p(3) =  0

So, 2 and 3 are zeroes or roots of the polynomial p(x).

Question 2 :

x² +4x+3  =  0 : x  = -1, 2

Solution :

Given that p(x)  =  x² +4x+3

p(-1) =  (-1)²+ 4(-1) +3

=   1-4+3

p(-1)  =  0

p(2)  =  2²+4(2)+3

=  4+8+3

p(2)  =  11 ≠ 0

So, -1 is a zero of the polynomial and 2 is not a zero.

Question 3 :

x³ -2x²-5x+6  =  0 : x  = 1, -2, 3

Solution :

Given that p(x)  =  x³ -2x²-5x+6

p(-1) =  x³ -2x²-5x+6

p(1) =  (1)³ -2(1)²-5(1) +6

=  1-2-5+6

p(-1)  = 0

p(-2) =  (-2)³ -2(-2)²-5(-2) +6

=  -8-8+10+6

=  -16+16

p(-2)  =  0

p(3) =  3³ -2(3)²-5(3) +6

=  27-18-15+6

=  33-33

p(3)  =  0

So, -1, -2 and 3 are zeroes or roots of the given polynomial.

Question 4 :

x³-2x²-x+2  =  0:     x =  -1, 2

Solution :

Given that p(x)  =  x³-2x²-x+2

p(-1) =  x³-2x²-x+2

p(-1) =  (-1)³ -2(-1)²-(-1)+2

=  -1-2+1+2

=  -3+3

p(-1)  =  0

p(2) =  2³ -2(2)²-2+2

=  8-2(4)-2+2

=  8-8-2+2

p(2)  =  0

So, -1 and 2 are zeroes of the polynomial.

Question 5 :

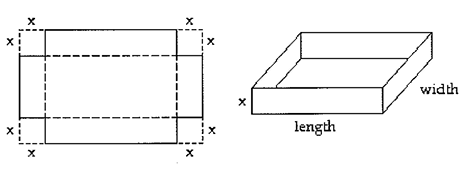
A box with an open top is formed by cutting out of the corners of a rectangular piece of cardboard and then folding up the sides. If x represents the length of side of the square cut from each corner and if the original piece of cardboard is 16 inches by 9 inches, what size must be cut off if the volume of the box is 120 cubic inches ?

Solution :

Length of cardboard = 16 inches

After we cut x inches on both sides, the new length

= 16 - 2x

Width of the cardboard = 9 inches

After we cut x inches on both sides, the new width

= 9 - 2x

Volume of the box = length x width x height 

= (16 - 2x) (9 - 2x) x

= x(144 - 18x - 32x + 4x²)

= x(144 - 50x + 4x²)

4x³ - 50x² + 144x = 120

4x³ - 50x² + 144x - 120 = 0

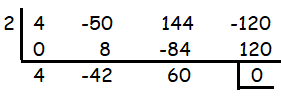
When x = 2, we get the remainder as 0. Then 2 is one of the zeroes of the polynomial.

So, length of side of square to cut from the box is 2 inches.

Find an nth degree polynomial function with real coefficients satisfying the given condition.

Question 6 :

Degree n = 3, 3 and i are zeroes of polynomial and f(2) = 25

Solution :

Zeroes of polynomial with highest exponent = 3.

Since i is one of the zeroes of the polynomial, then its conjugate -i will be other zero.

Let α = i and β = -i

Quadratic equation with the roots α and β is 

x² - (α+β)x + α β = 0

α+β = i - i ==> 0

αβ = i(i) = i² ==> -1

x² - 0x + (-1) = 0

x² - 1 = 0

The required cubic polynomial will have other root which is given as 3. So, other factor is (x - 3)

Multiplying these factors, we get

(x² - 1)(x - 3) = 0

x³ - 3x² - x + 3 = 0

Question 7 :

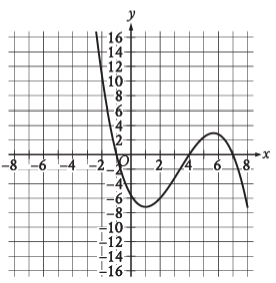
The graph y = f(x) is shown where the function f is defined b y f(x) = ax³ + bx² + cx + d and a, b, c and d are constants. For how many values of x does f(x) = 0 ?

a) one    b)  two     c) three    d) four

Solution :

Every cubic polynomial will have 3 zeroes.

Another name of zeroes :

Solutions, roots, x-intercepts 

By observing the graph, the curve is intersecting the graph at three different values -1, 4 and 7.

So, the answer is three, option c is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.