BINOMIAL EXPANSION PRACTICE WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Binomial expansion for (x + a)n is,
nc0xna0 + nc1xn-1a1 + nc2xn-2a2 + .........+ ncnxn-na0(
If X is a set containing n elements, then we know that nCr is the number of subsets of X having exactly r elements. So by adding nCr for r = 0, 1, 2, . . . , n we get the number of subsets of X. So by using the above identity we see that a set of n elements has 2n subsets.
(1) Expand (i) [2x2 − (3/x)]3 Solution
(ii) (2x2 − 3√1 − x2)4 + (2x2 + 3√1 − x2)4 Solution
(2) Compute (i) 1024 (ii) 994 (iii) 97 Solution
(3) Using binomial theorem, indicate which of the following two number is larger: (1.01)1000000, 10000.
(4) Find the coefficient of x15 in (x2 + (1/x3))10 Solution
(5) Find the coefficient of x6 and the coefficient of x2 in (x2 - (1/x3))6 Solution
(6) Find the coefficient of x4 in the expansion of (1 + x3)50(x2 + 1/x)5. Solution
(7) Find the constant term of (2x3 - (1/3x2))5 Solution
(8) Find the last two digits of the number 3600 Solution
(9) If n is a positive integer, show that, 9n+1 − 8n − 9 is always divisible by 64. Solution
(10) If n is an odd positive integer, prove that the coefficients of the middle terms in the expansion of (x + y)n are equal. Solution
(11) If n is a positive integer and r is a non negative integer, prove that the coefficients of xr and xn−r in the expansion of (1 + x)n are equal Solution
(12) If a and b are distinct integers, prove that a − b is a factor of an − bn, whenever n is a positive integer. [Hint: write an = (a − b + b)n and expand] Solution
(13) In the binomial expansion of (a + b)n, the coefficients of the 4th and 13th terms are equal to each other, find n. Solution
(14) If the binomial coefficients of three consecutive terms in the expansion of (a + x)n are in the ratio 1 : 7 : 42, then find n. Solution
(15) In the binomial coefficients of (1 + x)n, the coefficients of the 5th, 6th and 7th terms are in AP. Find all values of n. Solution
(16)
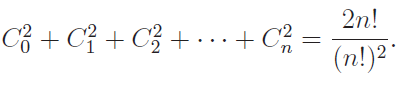
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

