BINOMIAL EXPANSION PRACTICE QUESTIONS

Question 1 :

If a and b are distinct integers, prove that a − b is a factor of aⁿ − bⁿ, whenever n is a positive integer. [Hint: write aⁿ = (a − b + b)ⁿ and expand]

Solution :

aⁿ  =  [(a - b) + b]ⁿ

aⁿ =  ⁿC₀(a-b)ⁿ+ⁿC₁(a-b)^n-1b¹+ⁿC₂(a-b)^n-2b²+ⁿC_n-1(a-b)b^n-1+ ⁿC_nbⁿ

aⁿ - bⁿ  = (a-b)ⁿ+ⁿC₁(a-b)^n-1b¹+ⁿC₂(a-b)^n-2b²+ⁿC_n-1(a-b)b^n-1

aⁿ - bⁿ 

= (a-b) { (a-b)^n-1 + ⁿC₁(a-b)^n-2b + ⁿC₂(a-b)^n-3b² + ⁿC_n-1b^n-1 }

Hence a − b is a factor of aⁿ − bⁿ, whenever n is a  positive integer.

Question 2 :

In the binomial expansion of (a + b)ⁿ, the coefficients of the 4^th and 13^th terms are equal to each other, find n.

Solution :

The coefficients of the fourth ad thirteenth terms in the binomial expansion of (a + b)ⁿ are ⁿC₃ and ⁿC₁₂ respectively.

Coefficient of 4^th term in (a+b)ⁿ = coefficient of 13^th term in (a + b)ⁿ

ⁿC₃  =  ⁿC₁₂ 

If ⁿC_x  =  ⁿCy   ==>  x = y or x + y = n 

n  =  15

Question 3 :

If the binomial coefficients of three consecutive terms in the expansion of (a + x)ⁿ are in the ratio 1 : 7 : 42, then find n.

Solution :

Let the three consecutive terms be r^th, (r+1)^th and (r+2)^th terms.Their coefficients in the expansion of (1+x)n are ⁿC_r-1, ⁿC_r and ⁿC_r+1 respectively. It is given that,

ⁿC_r-1 : ⁿC_{r :} ⁿC_r+1  = 1  :  7  :  42

ⁿC_{r-1 /} ⁿC_r  =  1 / 7

r/(n-r+1)  =  1/7

n - 8r + 1 = 0  ----(1)

 ⁿC_{r :} ⁿC_r+1  =  7/42

r+1/n-r  =  1/6

n - 7r - 6  =  0  -----(2)

(1) - (2)  ==>  (n - 8r + 1) - (n - 7r - 6)  =  0

  n - n - 8r + 7r + 1 + 6  =  0

  -r + 7  =  0  ==> r  =  7

By applying the value of r in the 1st equation, we get 

n - 8(7) + 1 = 0

n - 56 + 1  =  0

n  =  55

Hence the values of n and r are 55 and 7 respectively.

Question 4 :

In the binomial coefficients of (1 + x)ⁿ, the coefficients of the 5th, 6th and 7th terms are in AP. Find all values of n.

Solution :

The coefficients of 5^th, 6^th and 7^th terms in the binomial expansion of (1+x)ⁿ are ⁿC₄, ⁿC₅ and ⁿC₆ respectively,We are given that 

2 ⁿC₅  =  ⁿC_{4 +} ⁿC₆

2  =  (ⁿC₄)/(ⁿC₅)  + (ⁿC₆)/(ⁿC₅)

2  =  5/(n-4) + (n-5)/6

2  =  [30 + (n-4)(n-5)]/[6(n-4)]

12(n-4)  =  =  [30 + (n² - 4n - 5n + 20)]

12n - 48  =  30 + n² - 9n + 20

n² - 9n + 20 - 12n + 48 + 30  =  0 

n² - 21n + 98  =  0 

(n - 14) (n - 7)  =  0

n - 14 = 0   n - 7 = 0

n  =  14,  n  =  7

Question 5 :

Prove that

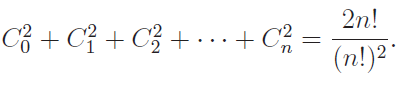
Solution :

n ^C ₀  =  C_{0 ,} n ^C ₁  =  C_{1 ,...............}

L.H.S

  =  (C₀)²+ (C₁)² + (C₂)² + .............  + (C_n)²

  =  (n^C₀)² + (n^C₁)² + (n^C₂)² + .................. + (n ^C _n)²

  =  (n^C₀)(n^C₀) + (n^C₁)(n^C₁) + (n^C₂)(n^C₂) + ................. (n^C_n)(n^C_n)

  =  (n^C ₀)(n^C_n-0) + (n^C₁)(n^C_n-1) + (n^C₂)(n^C_n-2) + ................. (n^C_n)(n^C_n-n)   -----(A)

(1 + x)ⁿ  =  n^C_{0 1}ⁿ x⁰ + n^C_{1 1}^n-1 x¹ + n^C_{2 1}^n-

² x² + ..........+ n^C_{n-1 1}^n-1 x^{n-1 +} n^C_{n 1}^n-nxⁿ

(1 + x)ⁿ  =  n^C₀ + n^C₁ x¹ + n^C₂ x² + ..........+ n^C_n-1 x^{n-1 +} n^C_n xⁿ  ----(1)

By writing the expansion in reverse order, we get

(1 + x)ⁿ  =  n^C_n xⁿ + n^C_n-1 x^n-1+ ..........+ n^C₁ x¹  + n^C₀---(2)

(1) ⋅ (2) 

(1 + x)²ⁿ  =  n^C₀ n^C_n + n^C₁ n^C_{n-1 + ..................... +} n^C₁ n^C_n-1 + n^C₀ n^C_n  ----(B)

Since (A) and (B) are equal, we may consider the simplified value of L.H.S is (1 + x)²ⁿ

T_{r + 1}   =   n ^C _r x^n-r a^r

x  =  1, a  =  x and n  =  2n

T_{r + 1}   =   2n ^C _r 1^2n-r x^r

here r  =  n

T_{n + 1}   =   2n ^C _n 1^2n-n xⁿ

  =  2n!/n(2n-n)! 1ⁿ xⁿ

Coefficient of xⁿ  =  (2n)!/(n!)²

Hence proved.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.