AREA BETWEEN TWO CURVES USING INTEGRATION WORKSHEET

(1)  Find the area of the region bounded by the line

x - y = 1 

x - axis x = 2 and x = 4             Solution

(2)  Find the area of the region bounded by the line

x - y = 1 

x - axis , x = - 2 and x = 0           Solution

(3)  Find the area of the region by the line

x - 2y - 12  =  0

and  y - axis, y = 2 and y = 5.              Solution

(4)  Find the area of the region bounded by the line

y = x - 5

and the x - axis between the ordinates x = 3 and x = 7.

Solution

(5)  Find the area of the region bounded by

x²  =  36y 

y - axis , y = 2 and y = 4              Solution

(6)  Find the area included between the parabola

y²  =  4ax

and its latus rectum.               Solution

(7)  Find the area of the region bounded by the ellipse

(x²/9) + (y²/5)  =  1

between the two latus rectum.             Solution

(8)  Find the area of the region bounded by the parabola

y²  =  4x

and the line

2x - y = 4

Solution

(9)  In the figure given below, the equation of the solid parabola is y  =  x² - 3 and the equation of the dashed line is y  =  2x. Determine the area of the shaded region.

Solution

(10)  Determine the area of the shaded region bounded by

y  =  -x² + 7x and y  =  x² - 5x

Solution

(11)  In the graph given below, the equation of the parabola is

x  =  (y-2)²/2

and the equation of the line

y  =  6-x.

Determine the area of the shaded region.

Solution

(12)  Find the common area enclosed by the parabolas

4y²  =  9x

and

3x²  =  16y

Solution

(13)  Find the area of the circle whose radius is a

Solution

Problem 1 :

Find the area of the region bounded by the line y = x - 3, x = 1, x = 5 and x-axis.

Solution

Problem 2 :

Find the area of the region bounded by y = x² - 5x + 4, x = 2, x = 3 and x-axis.

Solution

Problem 3 :

Find the area bounded by the curve y = sin(2x) between the ordinates x = 0, x = π and x-axis.

Solution

Problem 4 :

Find the area bounded by the curve y = x² - x - 2, x-axis, x = -2, and x = 4.

Solution

Find the area between the line and curve whose equations are given below.

y = x + 1

y = x² - 1

Solution

Problem 2 :

Find the area bounded by the curve and line whose equation are given below.

y = x³

y = x

Solution

Problem 3 :

Find the area of the region enclosed by the curve and the line whose equations are given below.

y² = x

y = x - 2

Solution

Example 4 :

Find the area of the region common to the circle and parabola whose equations are given below.

x² + y² = 16

y² = 6x

Solution

Example 5 :

Compute the area between the curve y = sin x and y = cosx and the lines x = 0 and x = π.

Solution

Problem 1 :

Find the area of the region described.

Solution

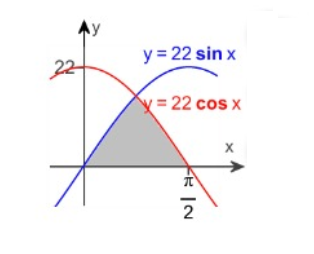
Problem 2 :

In the figure given below the equation of the solid curve is y  =  sec²x/4 and the equation of the dashed curve is y  =  4 cos²x. Determine the area of the shaded region.

Solution

Problem 3 :

Find the area of the region enclosed by the curves y  =  cos x and y  =  cos 2x for 0 ≤ x ≤ π 

Solution

(1)  Integrate the following with respect to x

∫ [(x + 4)⁵ + 5/(2 - 5x)⁴ - cosec²(3x - 1)] dx

Solution

(2)  Integrate the following with respect to x

∫ [4 cos (5-2x) + 9e^3x-6 + 24/(6-4x)] dx

Solution

(3)  Integrate the following with respect to x

∫ [sec²(x/5) + 18 cos 2x  + 10 sec (5x + 3) tan (5x + 3)] dx

Solution

(4)  Integrate the following with respect to x

∫ [8/√(1 - (4x)²) + 27/√(1 - 9x²) - 15/(1+25x²)] dx

Solution

(5)  Integrate the following with respect to x

∫ [6/(1 + (3x + 2)²)] - [12/√1 - (3-4x)²] dx

Solution

(6)  Integrate the following with respect to x

∫ (1/3) cos ((x/3) - 4)) + 7/(7x+9) + e^{(x/5) + 3} dx

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.