AREA BETWEEN TWO CURVES INVOLVING TRIG FUNCTIONS

Example 1 :

Find the area of the region described.

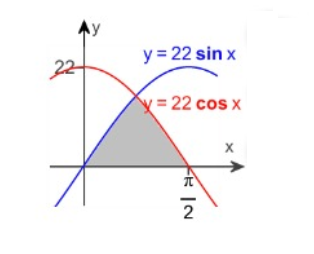
Solution :

Let us find the point of intersection of the curves

y  =  22 sinx  ---(1)

y  =  22 cosx  ---(2)

(1)  =  (2)

sinx  =  cosx

x  =  π/4

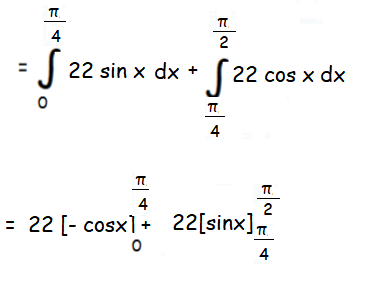
  =  22(-cosπ/4 + cos 0) + 22(sinπ/2 - sinπ/4)

  =  22(-1/√2 + 1) + 22(1 - 1/√2)

  =  22[-2/√2 + 2]

  =  22[-√2 + 2]

  =  22[2 - √2]

Example 2 :

In the figure given below the equation of the solid curve is y  =  sec²x/4 and the equation of the dashed curve is y   =  4 cos²x. Determine the area of the shaded region.

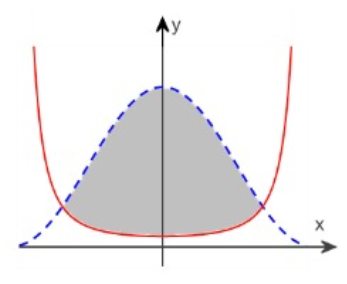
Solution :

y  =  sec²x/4 ----(1)

y  =  4 cos²x  ----(2)

(1)  =  (2)

sec²x/4  =  4 cos²x

1/cos²x  =  16 cos²x

1/cos⁴x  =  16

cos⁴x  =  1/16

cos x  =  ±1/2

x  =  cos^-1(1/2), x  =  cos^-1(-1/2)

x  =  -π/3 and x  =  π/3 

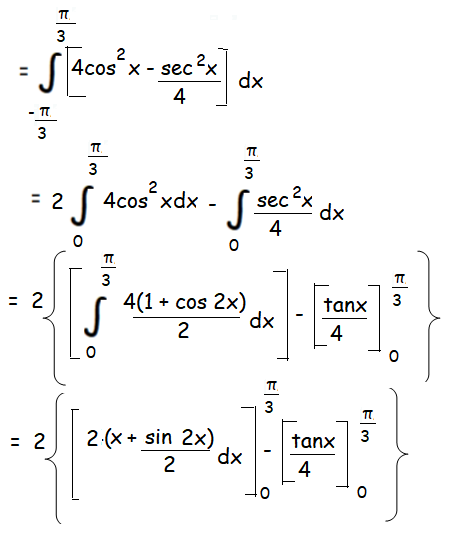
  =  2[2(π/3 + (sin2π/3)/2) - (tan π/3)]

  =  2[2π/3 + √3/2 - √3]

  =  [4π/3 + √3 - 2√3]

  =  [4π/3 - √3]

Example 3 :

Find the area of the region enclosed by the curves y  =  cos x and y  =  cos 2x for 0 ≤ x ≤ π 

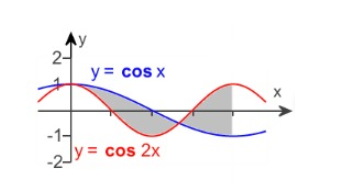
Solution :

y  =  cos x-----(1)

y  =  cos 2x -----(2)

(1)  =  (2)

cos x  =  cos 2x

cos x  =  2cos²x - 1

2cos²x - cosx - 1  =  0

Let t  =  cosx

2t² - t - 1  =  0

(2t + 1) (t - 1)  =  0

t  =  -1/2 and t  =  1

cos x  =  -1/2 and cos x  =  1

x  =  2π/3 and x  =  π

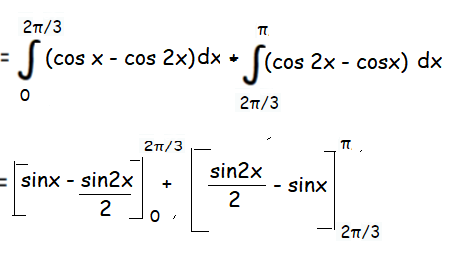
  =  sin 2π/3 - sin 2(2π/3)/2 - sin 2(2π/3)/2 + sin (2π/3)

  =  2(√3/2)-2(-√3/2)

  =  2√3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.