ADDING RATIONAL NUMBERS WITH DIFFERENT SIGNS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
Add (-4/5) and (+7/5).
Solution :
Step 1 :
Find the absolute difference of the rational numbers without the actual signs.
|4/5 - 7/5| = |-3/5| = 3/5
Step 2 :
In the given two rational numbers 4/5 and 7/5, the sign of the bigger number is positive. So, we have to take positive sign to the answer.
So,
(-4/5) + (+7/5) = +3/5
Example 2 :
Add (+5/9) and (-8/9).
Solution :
Step 1 :
Find the absolute difference of the rational numbers without the actual signs.
|5/9 - 8/9| = |-3/9| = 3/9 = 1/3
Step 2 :
In the given rational numbers 5 and 8, the sign of the bigger number is negative. So, we have to take negative sign to the answer.
So,
(+5/9) + (-8/9) = -1/3
Example 3 :
Add (+2.03) and (-2.3).
Solution :
Step 1 :
Find the absolute difference of the rational numbers without the actual signs.
|2.03 - 2.3| = |-0.27| = 0.27
Step 2 :
In the given rational numbers 2.03 and 2.3, the sign of the bigger number is negative. So, we have to take negative sign to the answer.
So,
(+2.03) + (-2.3) = -0.27
Example 4 :
Add 3 and -2 using a number line.
Solution :
Here, the rational numbers "3" and "-2" are having different signs.
To find the sum of rational numbers 3 and -2, we have to start at 3
Since the second number "-2" is negative, we have to move 2 units in the negative direction as given in the picture below.
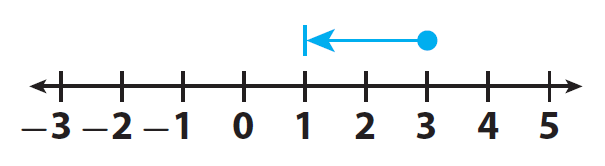
After having move 2 units in the negative direction, we are in the position of "1"
So,
3 + (-2) = 1
Example 5 :
During the day, the temperature increases by 4.5 degrees. At night, the temperature decreases by 7.5 degrees. What is the overall change in temperature?
Solution :
Step 1 :
Use a positive number to represent the increase in temperature and a negative number to represent a decrease in temperature.
Step 2 :
Find 4.5 + (-7.5).
Let us use the real number line to add 4.5 and (-7.5).
Step 3 :
Start at 4.5.
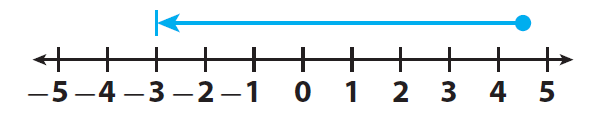
Step 4 :
Move | -7.5 | = 7.5 units to the left because the second addend is negative.
The result is -3.
The temperature decreased by 3 degrees overall.
Example 6 :
Ernesto writes a check for $2.50. Then he deposits $6 in his checking account. What is the overall increase or decrease in the account balance?
Solution :
Step 1 :
Use a positive number to represent a deposit and a negative number to represent a withdrawal or a check.
Step 2 :
Find -2.5 + 6.
Let us use the real number line to add -2.5 and 6.
Step 3 :
Start at -2.5.
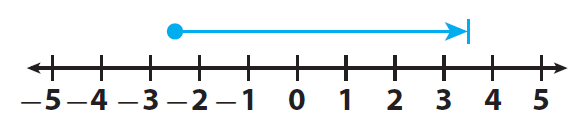
Step 4 :
Move | 6 | = 6 units to the right because the second addend is positive .
The result is 3.5.
The account balance will increase by $3.50.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
The Hidden Patterns in Hard SAT Math Questions
Feb 09, 26 06:45 PM
The Hidden Patterns in Hard SAT Math Questions -
AP Precalculus Problems and Solutions
Feb 09, 26 08:43 AM
AP Precalculus Problems and Solutions -
Dilation Transformation
Feb 07, 26 08:30 PM
Dilation Transformation - Concept - Rule - Examples with step by step explanation