HOW TO SOLVE POLYNOMIAL EQUATION OF DEGREE 5

To solve a polynomial equation of degree 5, we have to factor the given polynomial as much as possible. After having factored, we can equate factors to zero and solve for the variable.  

Example 1 :

Solve :

6x⁵ - x⁴ - 43x³ + 43x² + x - 6 = 0

Solution :

By trial and error, we can check the values 1 or -1 or 2 or -2...... as a zero for the above equation using synthetic division. 

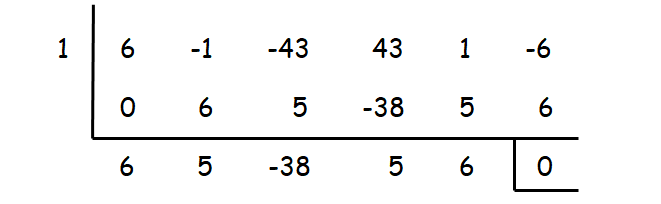
When we check with the value 1, we get remainder zero. So, x = 1 is one of the zeros. 

Resulting equation :

6x⁴ + 5x³ - 38x² + 5x + 6 = 0

Dividing both sides by x².

6x⁴/x² + 5x³/x² - 38x²/x² + 5x/x² + 6/x² = 0

6x² + 5x - 38 + 5/x + 6/x² = 0

6(x² + 1/x²) + 5 (x + 1/x) - 38 = 0 ----(1)

Let y = x + 1/x.

y² = (x + 1/x)²

y² = x² + 2(x)(1/x) + (1/x)²

y² = x² + 2 + 1/x²

y² - 2 = x² + 1/x²

(1)----> 6(y² - 2) + 5y - 38 = 0

6y² - 12 + 5y - 38 = 0

6y² + 5y - 50 = 0

6y² - 15y + 20 y - 50 = 0

3y(2y - 5) + 10(2y - 5) = 0

(3y + 10)(2y - 5) = 0

When y  =  -10/3,

(x² + 1)/x = -10/3

3(x² + 1) = -10x

3x² + 3 = -10x

3x² + 10x + 3 = 0

(3x + 1)(x + 3) = 0

x = -1/3 and 3

When y = 5/2,

x + 1/x = y

(x² + 1)/x = 5/2

2(x² + 1) = 5 x

2x² + 2 - 5x = 0

2x² - 5x + 2 = 0

(2x - 1)(x - 2) = 0

x = 1/2 and 2

Therefore the five zeros are 1, -1/3, 3, 1/2 and 2.

Example 2 :

Solve :

8x⁵ - 22x⁴ - 55x³ + 55x² + 22x - 8 = 0

Solution :

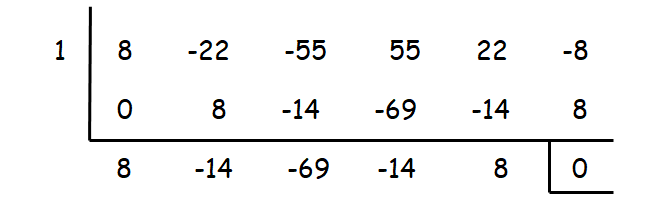
When we check with the value 1, we get remainder zero. So, x = 1 is one of the zeros. 

Resulting equation :

8x⁴ - 14x³ - 69x² - 14x + 8 = 0

Dividing both sides by x².

8x⁴/x² - 14x³/x² - 69x²/x² - 14x/x² + 8/x² = 0

8x² - 14x - 69 - 14/x + 8/x² = 0

8(x² + 1/x²) - 14(x + 1/x) - 69 = 0 ----(1)

Let y = x + 1/x. 

y² = (x + 1/x)²

y² = x² + 2(x)(1/x) + (1/x)²

y² = x² + 2 + 1/x²

y² - 2 = x² + 1/x²

(1)----> 8(y² - 2) - 14y - 69 = 0

8y² - 16 - 14y - 69 = 0

8y² - 14y - 85 = 0

(2y + 5)(4y - 17) = 0

When y = -5/2,

x + 1/x = y

(x² + 1)/x = -5/2

2(x² + 1) = -5x

2x² + 2 + 5x = 0

2x² + 5x + 2 = 0

2x² + 4x + 1x + 2 = 0

2x(x + 2) + 1(x + 2) = 0

(2x + 1)(x + 2) = 0

x = -1/2 and -2

When y = 17/4,

x + 1/x = y

(x² + 1)/x = 17/4

4(x² + 1) = 17x

4x² + 4 = 17x

4x² - 17x + 4 = 0

(4x - 1)(x - 4) = 0

x = 1/4 and 4

Therefore the five zeros are  1, -1/2, -2, 1/4 and 4.

Example 3 :

Solve :

6x⁵ + 11x⁴ - 33x³ - 33x² + 11x + 6 = 0

Solution :

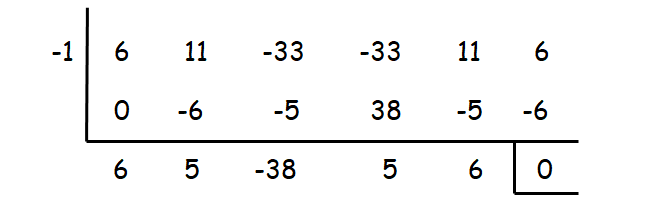
When we check with the value -1, we get remainder zero. So, x = -1 is one of the zeros. 

Resulting equation :

6x⁴ + 5x³ - 38x² + 5x + 6 = 0

Dividing both sides by x².

6x⁴/x² + 5x³/x² - 38x²/x² + 5x/x² + 6/x² = 0

6x² + 5x - 38 + 5/x + 6/x² = 0

6(x² + 1/x²) + 5(x + 1/x) - 38 = 0 ----(1)

Let y = x + 1/x. 

y² = (x + 1/x)²

y² = x² + 2(x)(1/x) + (1/x)²

y² = x² + 2 + 1/x²

y² - 2 = x² + 1/x²

(1)----> 6(y² - 2) + 5y - 38 = 0

6y² - 12 + 5y - 38 = 0

6y² + 5y - 50 = 0

6y² - 15y + 20y - 50 = 0

3y(2y - 5) + 10(2y - 5) = 0

(3y + 10)(2y - 5) = 0

When y = -10/3, 

x + 1/x = y

(x² + 1)/x = -10/3

3(x² + 1) = -10x

3x² + 3 = -10x

3x² + 10x + 3 = 0

3x² + 9x + x + 3 = 0

3x(x + 3) + 1(x + 3) = 0

(x + 3)(3x + 1) = 0

x = -3 and -1/3

When y = 5/2, 

x + 1/x = y

(x² + 1)/x = 5/2

2(x² + 1) = 5x

2x² + 2 - 5x = 0

2x² - 5x + 2 = 0

2x² - 4x - x + 2 = 0

2x(x - 2) - 1(x - 2) = 0

(2x - 1)(x - 2) = 0

x = 1/2 and 2

Therefore the five zeros are -1, -3, -1/3, 1/2 and 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.