WRITE THE QUADRATIC EQUATION IN VERTEX FORM

The vertex form of a quadratic function is

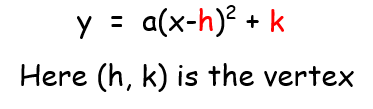
• If a > 0, then the parabola opens upward.
• If a < 0, then the parabola opens downward.

Write the following quadratics in vertex form  by completing the square and find the vertex.

Example 1 :

y  =  x² + 2x + 4

Solution :

Using completing the square method,

y  =  x² + 2⋅x⋅1 + 1² -1² + 4

y  =  (x+1)² -1² + 4

y  =  (x+1)² + 3

By comparing this with the vertex form of parabola, we get

(h, k)  ==>  (-1, 3)

Example 2 :

y = x²-6x + 3

Solution :

Using completing the square method,

y  =  x² - 2⋅x⋅3 + 3² - 3² + 3

y  =  (x-3)² -9 + 3

y  =  (x-3)² - 6

By comparing this with the vertex form of parabola, we get

(h, k)  ==>  (3, -6)

Example 3 :

y  =  x² - 2x

Solution :

Using completing the square method,

y  =  x² - 2⋅x⋅1 + 1² - 1²

y  =  (x-1)² -1

By comparing this with the vertex form of parabola, we get

(h, k)  ==>  (1, -1)

Example 4 :

y  =  x² - 3x + 1

Solution :

Using completing the square method,

y  =  x² - 2⋅x⋅(3/2) + (3/2)² - (3/2)²

y  =  (x-(3/2))² - (9/4)

By comparing this with the vertex form of parabola, we get

(h, k)  ==>  (3/2, -9/4)

Example 5 :

y  =  -x² + 2x + 8

Solution :

By factoring negative from the quadratic function, we get

y  =  -(x² - 2x - 8)

y  =  -(x² - 2x - 8)

y  =  -(x² - 2⋅x⋅1 + 1²-1-8)

y  =  -((x-1)²-9)

y  =  -(x-1)²+9

By comparing this with the vertex form of parabola, we get

(h, k)  ==>  (1, 9)

Example 6 :

y  =  (x-1)(x-3)

Solution :

y  =  x²-4x+3

y  =  x²-2⋅x⋅2+2²-2²+3

y  =  (x-2)²-4+3

y  =  (x-2)²-1

By comparing this with the vertex form of parabola, we get

(h, k)  ==>  (2, -1)

Example 7 :

y  =  3(x+1)²

Solution :

y  =  3(x+1)² + 0

(h, k)  ==> (-1, 0)

Example 8 :

Given f(x) = x² + 2x - 2, find the following.

a) y-intercept 

b)  the axis of symmetry

c)  The coordinate of vertex

d)  Identify the vertex as a maximum or minimum.

Solution :

a) y-intercept 

To find y-intercept, we put x = 0

Let y = x² + 2x - 2

When x = 0

y = 0² + 2(0) - 2

y = -2

b)  the axis of symmetry

By writing the quadratic equation in vertex form, 

y = x² + 2 x (1) + 1² - 1² - 2

y = (x + 1)² - 1 - 2

y = (x + 1)² - 3

(h, k) ==> (-1, -3)

Axis of symmetry x = -1

c)  The coordinate of vertex

Coordinate of vertex is at (-1, -3)

d)  Identify the vertex as a maximum or minimum.

Since the parabola opens up, it will have minimum at x = -1 and minimum value is -3.

Example 9 :

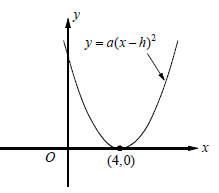
In the xy-plane, the parabola y = a (x - h)² has one x-intercept at (4, 0). If the y-intercept of the parabola is 9, what is the value of a ?

Solution :

By observing the picture given above, the x-intercept and vertex both are the same.

y = a (x - h)²

x-intercept is at (4, 0)

0 = a (4 - h)²

(4 - h)² = 0

4 - h = 0

h = 4

Applying the y-intercept, when x = 0, y = 9

y = a (x - 4)²

9 = a (0 - 4)²

9 = a (4)²

16a = 9

a = 9/16

So, the value of a is 9/16.

Example 10 :

In the xy-plane, if the parabola with equation

y = a(x + 2)² - 15

passes through (1, 3), what is the value of a ?

Solution :

y = a(x + 2)² - 15

Since the curve passes through the point (1, 3), we apply 

3 = a(1 + 2)² - 15

3 + 15 = a(3)²

18 = 9a

a = 18/9

a = 2

So, the value of a is 2.

Example 11 :

The graph of the y = a(x - 1)(x + 5) is the equation of the parabola with vertex (h, k). If the minimum value of y is -12. What is the value of a ?

Solution :

y = a(x - 1)(x + 5)

Since the zeroes are 1 and -5, midpoint of x-intercepts or zeroes the value of h.

= [1 + (-5)]/2

= -4/2

h = -2

When h = -2, then k = -12. So, the coordinate of vertex is at (-2, -12).

-12 = a(-2 - 1)(-2 + 5)

-12 = a(-3)(3)

-12 = -9a

a = 12/9

a = 4/3

So, the value of a is 4/3

Example 12 :

The xy-plane above shows two x-intercepts, a y-intercept, and vertex V of a parabola. Which of the following must be the coordinates of the vertex of the parabola?

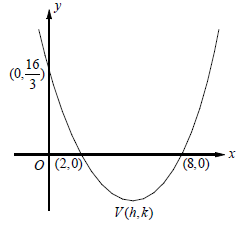
a)  V(5, -3)     b)  (5, -10/3)    c)  V(5, -8/3)    d) (5, -2)

Solution :

Vertex form of equation of parabola,

y = a (x - h)² + k

Midpoint of c-intercepts, 

= (2 + 8)/2

= 10/2

h = 5

y = a (x - 5)² + k

Since y-intercept is (0, 16/3), we get

16/3 = a (0 - 5)² + k

16/3 = 25a + k -----(1)

Applying the point (2, 0), we get

0 = a(2 - 5)² + k

0 = a(- 3)² + k

0 = 9a + k

k = -9a -----(2)

Applying k = -9a in (1), we get

16/3 = 25a + (-9a)

16/3 = 16a

a = 16/3(16)

a = 1/3

y = (1/3) (x - 5)² + k

applying the point (8, 0), we get

0 = (1/3) (8 - 5)² + k

0 = (1/3) (3)² + k

0 = 3 + k

k = -3

So, the vertex is (5, -3)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.