WORD PROBLEMS INVOLVING PERIMETER

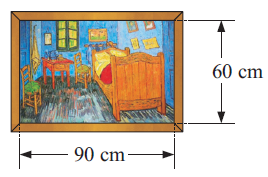
Problem 1 :

A rectangular painting 60 cm high and 90 cm wide is to be 5 cm wide wooden frame. Find the perimeter of 

(a)  the painting

(b)  the frame.

Solution :

Perimeter of painting  =  2(length + width)

Length  =  60 cm and width  =  90 cm

=  2(60+90)

=  2(150)

=  300 cm

Perimeter of the frame :

Width of the frame  =  5 cm

length of picture with frame  =  90+5+5

=  100 cm

width of picture with frame  =  60+5+5

=  70 cm

Perimeter of picture along with frame  =  2(100+70)

=  2(170)

=  340 cm

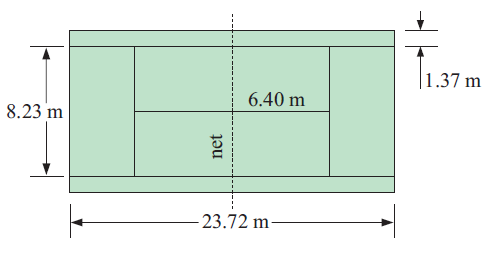
Problem 2 :

A tennis court has its lines marked as shown

(a)  Find the total length of the lines.

(b)  Find the length of the outer perimeter of the tennis court.

Solution :

(a)  Total length of lines 

=  4(23.72) + 4(8.23) + 4(1.37) + 2(6.40)

=  94.88 + 32.92 + 5.48 + 12.8

=  146.08 cm

(b)  Length of outer perimeter  =  2(length + width)

length  =  23.72

width  =  8.23 + 1.37 + 1.37

=  10.97

Perimeter  =  2(23.72 + 10.97)

=  2(34.69)

=  69.38 cm

Problem 3 :

A rectangular swimming pool is 22 meters by 8 meters. It is surrounded by a path one meter wide.

a) Draw and label a diagram of the pool and path.

b) Find the perimeter around the outside edge of the path.

Solution :

(a)  

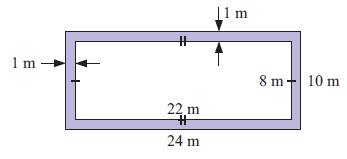
(b)  Length  =  24 m, width  =  10 m

Perimeter around the outside edge  =  2(24+10)

=  2(34)

=  68 cm

Problem 4 :

An equilateral triangular field has sides of length 380 meters. Find the cost of fencing the field with three strands of wire if the wire costs $1.18 per meter.

Solution :

Side length of equilateral triangle  =  380 meters

Cost of fencing wire  =  $1.18 per meter

Side length of equilateral triangular field  =  380 meter

Length of fencing  =  3(380)

=  1140 m

Length of fencing with three strands of wire  =  3(1140)

=  3420 meter

Required cost  =  1.18(3420)

=  $4035.6

Problem 5 :

A long distance runner trains by running around a 450 m by 1.25 km rectangular block. If he completes 12 laps in training, how far has he run?

Solution :

Length of block  =  450 m

=  0.45 km

Width  =  1.25 km

Perimeter of the block  =  2(0.45 + 1.25)

=  2(1.7)

=  3.4 km

Distance covered in 12 laps  =  12(3.4)

=  40.8 km

Problem 6 :

How long would it take a farmer to check the fences of a 680 m by 340 m rectangular paddock if 50 m can be checked every minute?

Solution :

Length of the fencing  =  680 m

width of the fencing  =  340 m

Perimeter of the fencing  =  2(680+340)

=  2(1020)

=  2040

It is being checked in every 50 m 

Time taken to check this  =  2040/50

=  204/5

=  4008 minutes

=  40 minutes 0.8(60 seconds)

=  40 minutes 48 seconds

Problem 7 :

Jason plans to build a picket fence 30 m long with the  design shown. There is a 2 m long post every 2 m, to which the rails are attached. The timber for the pickets costs $1:80 per meter, for the rails costs $2.50 per meter, and for the posts costs $4:50 per meter. Find:

a) the number of posts and hence the total length of  timber required for the posts

b) the total length of rails needed

c) the number of pickets needed

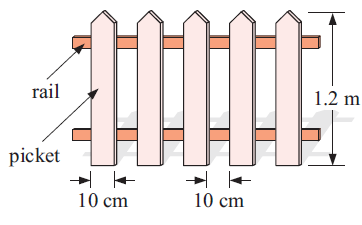
Solution :

Post is the vertical timber kept.

Width of the picket = 10 cm

height of picket = 1.2 m

Length of fence = 30 m = 3000 cm

Distance covered by 5 pickets = 100 cm

To cover 3000 cm distance, we need 5(30) which is 150 pickets.

Posts to be fixed for every 2 m, that is 200 cm

a)  In the 3000 cm distance, we can fix 3000/200 which is 15 posts. At last will fix one post, then the number of posts required is 16.

b) Distance to be covered for fence is 3000 cm which is 30 cm.

Length covered by one rail = 30 m

length covered by 2 rails = 2(30)

= 60 m

c)  In 100 cm length, we fix 5 pickets. To cover 3000 cm, we need

Let x be the number of pickets fixed.

100 : 5 = 3000 : x

100/5 = 3000/x

100x = 3000(5)

x = 15000/100

x = 150 pickets

length of picket = 1.2 m

width = 10 cm ==> 0.1 m

Problem 8 :

The width of a rectangle is 3 yards less than its length. The perimeter is 130 yards. Find the length and the width of the rectangle.

Solution :

Let x be the length of the rectangle.

Width = x - 3

Perimeter = 130 yards

2(x + x - 3) = 130

2x - 3 = 65

2x = 68

x = 34

So, the length of the rectangle is 34 yards

Width = 34 - 3

= 31 m

Problem 9 :

The length of the second side of a triangle is 2 inches less than the length of the first side. The length of the third side is 12 inches more than the length of the first side. The perimeter of the triangle is 73 inches. Find the length of each side of the triangle.

Solution :

Let x be the length of the first side

length of the second side = x - 2

length of the third side = x + 12

Perimeter = 73 inches

x + x - 2 + x + 12 = 73

3x + 10 = 73

3x = 73 - 10

3x = 63

x = 63/3

x = 21 cm

x - 2 ==> 19 cm

x + 12 = 21 + 12 ==> 33 cm

So, the side lengths of the triangle are 21 cm, 19 cm and 33 cm respectively.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.