Volume of Cylinders Spheres and Cones Word Problems

VOLUME OF CYLINDERS SPHERES AND CONES WORD PROBLEMS

(1) Find the volume of a solid cylinder whose radius is 14 cm and height is 30 cm.

(2) A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, then find the quantity of soup to be prepared daily in the hospital to serve 250 patients?

Solution

(3) The sum of the base radius and the height of a solid cylinder is 37 cm. If the total surface area of the cylinder is 1628 sq.cm, then find the volume of the cylinder.

Solution

(4) The volume of a cylindrical water tank is 1.078 × 10⁶ litres. If the diameter of the tank is 7 m, find its height.

Solution

(5) Find the volume of the iron used to make a hollow cylinder of height 9 cm and whose internal and external radii are 21 cm and 28 cm respectively.

Solution

(6) For the cylinders A and B

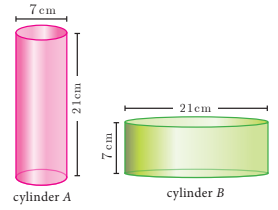
(i) find out the cylinder whose volume is greater.

(ii) verify whether the cylinder with greater volume has greater total surface area.

(iii) find the ratios of the volumes of the cylinders A and B.

Solution

(7) A 14 m deep well with inner diameter 10 m is dug and the earth taken out is evenly spread all around the well to form an embankment of width 5 m. Find the height of the embankment.

Solution

Answer Key

1) 18480 cubic.cm

2) 38.5 L

3) 4620 cm³

4) h = 28.02

5) 9693.18 cm³

6) i) Volume of cylinder A = 807.765 cm³

Volume of cylinder B = 2423.295 cm³

ii) Surface area of cylinder A = 538.51 cm²

Surface area of cylinder B = 1153.95 cm²

Cylinder B has greater volume and greater surface area.

iii) 1 : 3.

7) H = 4.67 m

(1) Volume of a solid cylinder is 62.37 cu.cm. Find the radius if its height is 4.5 cm.

Solution

(2) The radii of two right circular cylinders are in the ratio 2:3. Find the ratio of their volumes if their heights are in the ratio 5:3.

Solution

(3) The radius and height of two circular cylinders are in the ratio 5 : 7. If its volume is 4400 cu.cm, find the radius of the cylinder.

Solution

(4) A rectangular sheet of metal foil with dimension 66 cm x 12 cm is rolled to form a cylinder of height 12 cm. Find the volume of the cylinder.

Solution

(5) A lead pencil is in the shape of right circular cylinder. The pencil is 28 cm long and its radius is 3 mm. If the lead is of radius 1 mm, then find the volume of the wood used in the pencil.

Solution

(6) A cylindrical glass with diameter 20 cm has water to a height of 9 cm. A small cylindrical metal of radius 5 cm and height 4 cm is immersed completely. Calculate the raise of the water in the glass?

Solution

(7) A right circular cylindrical container of base radius 6 cm and height 15 cm is full of ice cream. The ice cream is to be filled in cones of height 9 cm and base radius 3 cm, having a hemispherical cap. Find the number of cones needed to empty the container.

Solution

(8) If the radius of the base of a right circular cylinder is halved keeping the same height, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is

(a) 1:2 (b) 1:4 (c) 1:6 (d) 1:8

Solution

Answer Key

1) r = 2.1 cm

2) 20 : 27

3) r = 10 cm

4) 4158 cm³

5) 7.04 cm³.

6) 1 cm.

7) Number of cones is 12.

8) 1 : 4

(1) Radius and slant height of a cone are 20 cm and 29 cm respectively. Find its volume.

(2) The circumference of the base of a 12 m high wooden solid cone is 44 m. Find the volume.

(3) A vessel is in the form of frustum of a cone. Its radius at one end and the height are 8 cm and 14 cm respectively. If its volume is 5676/3 cm³, then find the radius at the other end.

(4) The perimeter of the ends of a frustum of a cone are 44 cm and 8.4 Π cm. If the depth is 14 cm, then find its volume.

(5) You must answer a trivia question before the sand in the timer falls to the bottom. The sand falls at a rate of 50 cubic millimeters per second. How much time do you have to answer the question?

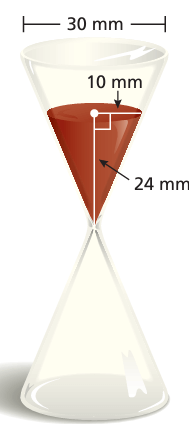
(6) The volume of a cone is 20π cubic meters. What is the volume of a cylinder having the same base and same height?

(7) Water leaks from a crack in a vase at a rate of 0.5 cubic inch per minute. How long does it take for 20% of the water to leak from a full vase?

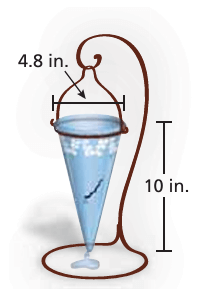
(8) You have 10 gallons of lemonade to sell. (1 gal ≈ 3785 cm³)

a. Each customer uses one paper cup. How many paper cups will you need?

b. The cups are sold in packages of 50. How many packages should you buy?

c. How many cups will be left over if you sell 80% of the lemonade?

Asnwer Key

1) Volume of the cone = 8800 cm³

2) Volume of the cone = 616 cm³

3) radius = 5 cm

4) Volume of the frustum cone = 1408.57 cm³

5) You have about 50 seconds to answer the question.

6) Volume of cylinder = 60π cubic units.

7) the time taken is 24 minutes

8) a) number of packs of cups required is 205.

b) 5 packages are needed.

c) 86 cups will be remaining.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.