VOLUME OF CYLINDER QUESTIONS AND ANSWERS

Question 1 :

Volume of a solid cylinder is 62.37 cu.cm. Find the radius if its height is 4.5 cm

Solution :

Height of solid cylinder  =  4.5 cm

Volume of cylinder  =  62.37 cu.cm

πr²h  =  62.37

 (22/7) ⋅ r²⋅4.5  =  62.37

r²  =  62.37 ⋅ (1/4.5) ⋅ (7/22)

r²  =  13.86 ⋅ (7/22)

r²  =  97.02/22

r²  =  4.41

r  =  √(2.1 ⋅ 2.1)

r  =  2.1 cm

Radius of the cylinder  =  2.1 cm

Question 2 :

The radii of two right circular cylinders are in the ratio 2:3. Find the ratio of their volumes if their heights are in the ratio 5:3.

Solution :

Let r₁ and r₂ are the radii of two cylinders.

Let h₁ and h₂ are the heights of two cylinders.

r₁ : r₂  =  2:3

r₁/r₂  =  2/3

r₁  =  2r₂/3

h₁ : h₂  =  5 : 3

h₁/h₂  =  5/3

h₁  =  5h₂/3

Volume of cylinder  =  πr²h

πr₁²h₁ : πr₂² h₂

(2r₂/3)² (5h₂/3) : r₂² h₂

 (4 r₂²/9)(5h₂/3) : r₂² h₂

20/27 : 1

20 : 27

Ratio of volume of two cylinders 20 : 27

Question 3 : 

The radius and height of two circular cylinders are in the ratio 5 : 7. If its volume is 4400 cu.cm, find the radius of the cylinder.

Solution :

Let r and h are the radius and height of cylinder

r : h  =  5 : 7

r/h  =  5/7

r  =  5h/7

Volume of the cylinder  =  4400 cu.cm

πr²h  =  4400

(22/7) (5h/7)² ⋅ h = 4400

(22/7) ⋅ (25h²/49) ⋅ h  =  4400

h³ = 4400 ⋅ (7/22) ⋅ (49/25)

h³  =  176 ⋅ (7/22) ⋅ 49

h³  =  8 ⋅ 7 ⋅ 7 ⋅ 7

h  =  14 cm

r  =  5(14)/7

r  =  10 cm

Radius of the cylinder = 10 cm.

Question 4 :

A rectangular sheet of metal foil with dimension 66 cm x 12 cm is rolled to form a cylinder of height 12 cm. Find the volume of the cylinder.

Solution :

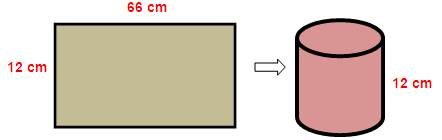
Length of metal sheet  =  66 cm

Width of sheet = 12 cm

Circumference of the base of the cylinder  =  66 cm

2πr  =  66

2 ⋅ (22/7) ⋅ r  =  66

r  =  66 ⋅ (1/2) ⋅ (7/22) 

r  =  3 ⋅ (1/2) ⋅ 7

r  =  21/2

r  =  10.5 cm

Volume of the right circular cylinder  =  πr²h

=  (22/7) ⋅ (10.5)² ⋅ 12

=  (22/7) ⋅ 10.5 ⋅ 10.5 ⋅ 12

=  4158 cm³

Volume of the the right circular cylinder = 4158 cm³

Question 5 :

A lead pencil is in the shape of right circular cylinder. The pencil is 28 cm long and its radius is 3 mm. If the lead is of radius 1 mm, then find the volume of the wood used in the pencil.

Solution :

Height of the pencil = 28 cm

Outer radius (R)  =  3 mm

Inner radius (r)  =  1 mm

Now we have to change the units from mm to cm. For that we have to divide it by 10.

R  =  3/10  =  0.3 cm

r  =  1/10

r  = 0.1 cm

To find the volume of the wood used to make that pencil, simply we can find the volume of the pencil. Pencil is in the shape of hollow cylinder

Volume of hollow cylinder  =  πh(R²-r²)

=   (22/7) ⋅ 28 ⋅ (0.3²-0.1²)

=  22 ⋅ 4 ⋅ (0.09-0.01)

=  7.04 cm³

Volume of wood used in the pencil  =  7.04 cm³.

Question 6 :

A cylindrical glass with diameter 20 cm has water to a height of 9 cm. A small cylindrical metal of radius 5 cm and height 4 cm is immersed completely. Calculate the raise of the water in the glass?

Solution :

Measurement of large cylindrical glass :

Radius r₁ = 20/2 ==> 10 cm

height = 9 cm (the total height)

Measurement of small cylindrical glass :

radius r₂ = 5 cm

height = 4 cm

Let H be the raised height

Quantity of water increased = volume of water of small cylindrical tank

πr₁² H = πr₂² h

10² H = 5² x 4

H = 100/100

H = 1

So, the raised height is 1 cm.

Question 7 :

A right circular cylindrical container of base radius 6 cm and height 15 cm is full of ice cream. The ice cream is to be filled in cones of height 9 cm and base radius 3 cm, having a hemispherical cap. Find the number of cones needed to empty the container.

Solution :

Radius = 6 cm

Height = 15 cm

Quantity of ice cream in cylindrical container = πr² h

= 3.14 x 6² x 15

= 1695.6 cm³

Volume of cone + hemispherecial cap

Radius of cone = 3 cm, height = 9 cm

= (1/3) πr² h + (2/3) πr³

= (1/3) πr²(h + 2r)

= (1/3) x 3.14 x 3²(9 + 2(3))

= (1/3) x 3.14 x 3²(9 + 6)

= (1/3) x 3.14 x 3² x 15

= 141.3 cm³

Number of cones needed to empty the container

= 1695.6/141.3

= 12

So, the required number cones is 12.

Question 8 :

If the radius of the base of a right circular cylinder is halved keeping the same height, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is

(a) 1:2    (b) 1:4    (c) 1:6    (d) 1:8

Solution :

Let r be the radius of cylinder

Radius of new cylinder = r/2

Let h be the height of both cylinder.

π(r/2)²h : πr²h

(r²/4) : r²

1 : 4

So, the required ratio is 1 : 4, option b is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.