EXAMPLES ON VOLUME OF CYLINDER

We can find the volume V of both a prism and a cylinder by multiplying the height by the area of the base. 

Let the area of the base of a cylinder be B and the height of the cylinder be h. Write a formula for the cylinder’s volume V.

V = Bh

The base of a cylinder is a circle, so for a cylinder,

B = πr²

Then, we have

V = πr²h cubic units

Example 1 :

Find the volume of a solid cylinder whose radius is 14 cm and height is 30 cm.

Solution :

We need to find the volume of the solid cylinder.

Radius of the cylinder  =  14 cm

Height of the cylinder  =  30 cm

Volume of the right circular cylinder  = πr²h

=  (22/7) · (14)² · 30

=  (22/7) · 14  · 14 · 30

=  18480 cubic.cm

Volume of the cylinder  =  18480 cubic.cm

Example 2 :

A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, then find the quantity of soup to be prepared daily in the hospital to serve 250 patients?

Solution :

Radius of the cylinder  =  7/2 cm

Height of the cylinder  =  4 cm

To find quantity of soup in one bowl,  we have to find the quantity of each bowl.

Volume of the right circular cylinder  =  πr²h

=  (22/7) · (7/2)²  · 4

=  (22/7) · (7/2) · (7/2) · 4

=  154 cm³

Volume of soup in one cylindrical bowl  =  154 cm³

Volume of soup in 250 cylindrical bowl  =  250 · 154

=  38500 cm³

1000 cm³  =  1 L

Therefore required quantity of soup  =  38500/1000

=  38.5 L

Required quantity of soup for 25 patients = 38.5 L

Example 3 :

The sum of the base radius and the height of a solid cylinder is 37 cm. If the total surface area of the cylinder is 1628 sq.cm, then find the volume of the cylinder.

Solution :

Let r and h are the radius and height of the cylinder respectively

Sum of radius and height  =  37

r + h  =  37 cm

Total surface area of cylinder  =  1628 sq.cm

2πr(h + r)  =  1628

2πr(37)  =  1628

2πr  =  1628/37

2 · (22/7) · r = 44

r  =  44 · (1/2) · (7/22)

r  =  7

7 + h  =  37

h  =  30 cm

Volume of the right circular cylinder =  πr²h

=  (22/7) ·7²·30

=  (22) x (7) x (30)

=  4620 cm³

Volume of cylinder  =  4620 cm³

Example 4 :

The volume of a cylindrical water tank is 1.078 × 10⁶ litres. If the diameter of the tank is 7 m, find its height.

Solution :

Volume of cylinder = 1.078 × 10⁶

1000 liter = 1 m³

Diameter = 7 m

= 1.078 × 10³ x 10³

= 1078

radius = 3.5 m

πr²h = 1078

3.14 x 3.5² x h = 1078

h = 1078 / (3.14 x 3.5²)

= 1078 / (3.14 x 12.25)

h = 28.02

Example 5 :

Find the volume of the iron used to make a hollow cylinder of height 9 cm and whose internal and external radii are 21 cm and 28 cm respectively.

Solution :

Height (h) = 9 cm

External radius (R) = 28 cm

Internal radius (r) = 21 cm

Volume = πh(R² - r²)

= 3.14 x 9 x (28² - 21²)

= 3.14 x 9 x (784 - 441)

= 3.14 x 9 x 343

= 9693.18 cm³

Example 6 :

For the cylinders A and B

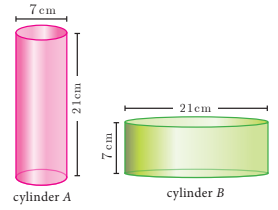
(i) find out the cylinder whose volume is greater.

(ii) verify whether the cylinder with greater volume has greater total surface area.

(iii) find the ratios of the volumes of the cylinders A and B.

Solution :

i) 

Volume of cylinder A = πr²h

Radius = 7/2 ==> 3.5 cm, height (h) = 21 cm

= 3.14 x 3.5² x 21

= 807.765 cm³

Volume of cylinder B = πr²h

Radius = 21/2 ==> 10.5 cm, height (h) = 7 cm

= 3.14 x 10.5² x 7

= 2423.295 cm³

Cylinder B is greater.

ii) 

Total surface area of cylinder A = 2πr(h + r)

= 2 x 3.14 x 3.5 (21 + 3.5)

= 21.98(24.5)

= 538.51 cm²

Approximately the surface area of cylinder A is 539 cm²

Total surface area of cylinder B = 2πr(h + r)

= 2 x 3.14 x 10.5 (7 + 10.5)

= 65.94(17.5)

= 1153.95 cm²

Cylinder B has greater volume and greater surface area.

iii)  Volume of cylinder A / Volume of cylinder B

= 808/2423

= 1/3

So, the required ratio is 1 : 3.

Example 7 :

A 14 m deep well with inner diameter 10 m is dug and the earth taken out is evenly spread all around the well to  form an embankment of width 5 m. Find the height of the embankment.

Solution :

height = 14 m

External radius (R) = ?

Inner radius (r) = 10/2 ==> 5 m

Width = 5 m

Width = R - r

5 = R - 5

R = 10 m

Volume of earth in the enbankment = Volume of the well

πh(R² - r²) = πr²h

H x (10² - 5²) = 5²x14

H = (25 x 14)/(100 - 25)

= 350/75

H = 4.67 m

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.