VOLUME OF COMPOSITE SOLIDS

Example 1 : 

Allie has two aquariums connected by a small square prism. Find the volume of the double aquarium.

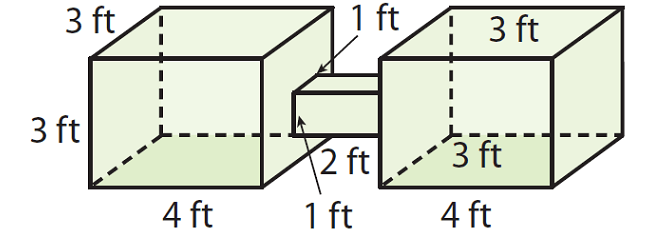
Solution :

Step 1 :

Find the volume of each of the larger aquariums.

Volume  =  Base area x Height

Volume  =  (4 x 3) x 3

Volume  =  12 x 3

Volume  =  36 cubic ft. 

Step 2 :

Find the volume of the connecting prism.

Volume  =  Base area x Height

Volume  =  (2 x 1) x 1

Volume  =  2 x 1

Volume  =  2 cubic ft.

Step 3 :

Add the volumes of the three parts of the aquarium.

V  =  36 + 36 + 2

V  =  74 cubic ft.

The volume of the aquarium is 74 cubic ft.

Example 2 : 

The figure is composed of a rectangular prism and a triangular prism. Find the volume of the figure.

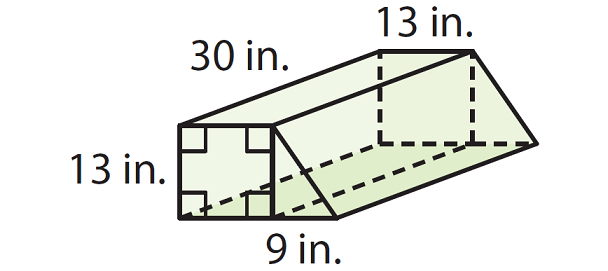
Solution :

Step 1 :

Find the volume of each of the larger aquariums.

Volume  =  Base area x Height 

Volume  =  (30 x 13) x 13

Volume  =  5070 cubic in.

Step 2 :

Find the volume of the triangular prism.

Volume  =  (1/2) x Base area x Height 

Volume  =  (1/2) x (30 x 9) x 13

Volume  =  1755 cubic in.

Step 3 :

Add the volumes of the two parts of the aquarium.

V  =  5070 + 1755

V  =   6825 cubic in.

The volume of the given figure is 6825 cubic in.

Example 3 : 

The figure is composed of a rectangular prism and a triangular prism. Find the volume of the figure.

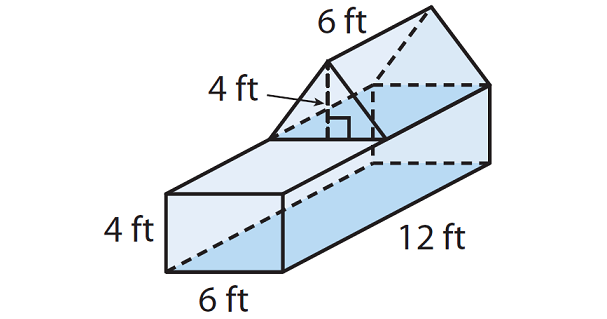
Solution :

Step 1 :

Find the volume of each of the larger aquariums.

Volume  =  Base area x Height 

Volume  =  (12 x 6) x 4

Volume  =  288 cubic ft.

Step 2 :

Find the volume of the triangular prism.

Volume  =  (1/2) x Base area x Height 

Volume  =  (1/2) x (6 x 6) x 4

Volume  =  72 cubic ft.

Step 3 :

Add the volumes of the two parts of the aquarium.

V  =  288 + 72

V  =   360 cubic ft.

The volume of the given figure is 360 cubic ft.

Example 4 : 

A wooden box is in the shape of a regular pentagonal prism. The sides, top, and bottom of the box are 1 centimeter thick. Approximate the volume of wood used to construct the box. Round your answer to the nearest tenth.

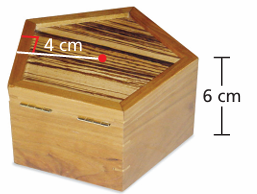
Solution :

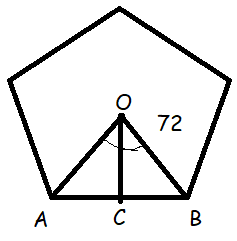
<COB = 72/2 ==> 36

OC = 4 cm, BC = ?

tan 36 = opposite side / adjacent side

tan 36 = BC/OC

tan 36 = BC/4

BC = 4(tan 36)

= 4(0.726)

BC = 2.904

AB = 2(2.904) ==> 5.808 cm

Side length of the pentagon = 5.808 cm

Volume of the prism = (1/2) x perimeter x apothem x height of the prism

= (1/2) x 5(5.808) x 4 x 6

= 348.48 cm³

So, the required volume of the pentagonal shape prism is 348.48 cm³

Example 5 :

A barn is in the shape of a pentagonal prism with the dimensions shown. The volume of the barn is 9072 cubic feet. Find the dimensions of each half of the roof.

Solution :

Volume of the barn = 9072 cubic inches

Volume of rectangular prism + volume of triangular prism = 9072

Volume of isosceles triangular base prism = (1/2) ⋅ x ⋅ x

36 x 18 x 8 + (1/2) ⋅ x ⋅ x ⋅ 36 = 9072

5184 + 18x² = 9072

18x² = 9072 - 5184

18x² = 3888

x² = 3888/18

x² = 216

x = 14.69

Example 6 :

You drill a circular hole of radius r through the base of a cylinder of radius R. Assume the hole is drilled completely through to the other base. You want the volume of the hole to be half the volume of the cylinder. Express r as a function of R.

Solution :

Volume of cylinder = πR²h

Radius of hole = r

Volume of hole = 1/2 of volume of cylinder

πr²h = (1/2) x πR²h

r² = (1/2) x R²

r = (1/√2)R

Example 7 :

How can you change the height of a cylinder so that the volume is increased by 25% but the radius remains the same?

Solution :

Let r and h be the radius and height of the cylinder respectively.

New radius will be increased by 25%, then new radius = 125% of r

volume of cylinder = πR²h

= π (125% of r)²h

= π (1.25 r)²h

= π (1.5625 r²)h

= 1.5625 π r²h

= 156.25% of π r²h

So, the volume of new cylinder will be increased by 56.25% of old cylinder.

Example 8 :

How can you change the edge length of a cube so that the volume is reduced by 40%?

Solution :

Let a be the side length of the cube.

Let A be the side length of new cube.

Volume of cube = a³

After decrease of 40%, the new volume = 60% of a³

A³ = 0.60a³

A = ∛0.60a³

A = 3.91 of a

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.