VOLUME OF COMBINATION OF SOLIDS PROBLEMS

Problem 1 :

A hollow cylindrical pipe is of length 40 cm. Its internal and external radii are 4 cm and 12 cm respectively. It is melted and cast into a solid cylinder of length 20 cm. Find the radius of the new solid.

Solution :

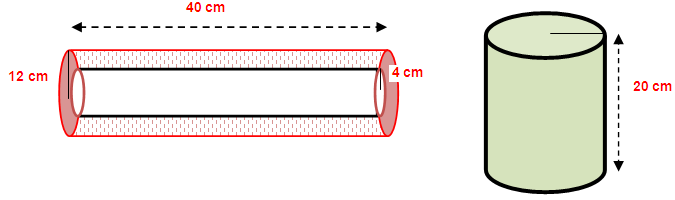
length of cylindrical pipe (h) = 40 cm

internal radius of the pipe (r) = 4 cm

external radius of the pipe (R) = 12 cm

Height of cylinder = 20 cm

Volume of hollow cylindrical pipe = Volume of cylinder

Π h (R² - r²) =  Π r² h

h (R² - r²)  =   r² h

(40) (12² - 4²)  =  r² (20)

(40) (144 - 16) =  r² (20)

(40) (128)/20  =  r²

r²  =  (40) (128)/20

r²  =  2 (128)

r  =  √256

r  =  16 cm

Therefore radius of cylinder  =  16 cm

Problem 2 :

An iron right circular cone of diameter 8 cm and height 12 cm is melted and recast into spherical lead shots each of radius 4 mm. How many lead shots can be made?

Solution :

diameter of right circular cone = 8 cm

radius of right circular cone (r) = 4 cm

Height of right circular cone (h) = 12 cm

Radius of spherical lead shot (r) = 4 mm

10 mm  =  1 cm

4 mm  =  (4/10) cm 

Volume of right circular cone

= n x (Number of spherical lead shots)

n  =  Volume of cone/Number of spherical lead shots

n  =   (1/3)Π r² h/(4/3)Π r³

n  =  (1/3) (4)² (12) x (3/4) (10/4)³

n =  3 x 5 x 5 x 10

n = 750 lead shots

Therefore 750 lead shots can be made.

Problem 3 :

A container with a rectangular base of length 4.4 m and breadth 2 m is used to collect rain water. The height of the water level in the container is 4 cm and water is transferred into a cylindrical vessel with radius 40 cm. What will be the height of the water level in the cylinder?

Solution :

Volume of water in cuboidal container  =  Volume of water in cylindrical container

lwh  =  Π r²h

l  =  4.4 m, w  =  2 m, h  =  4 cm ==>  4/100 ==>  1/25 m

r  =  40 cm ==>  40/100

4.4(2) (1/25)  =  Π (2/5)²h

h  =  4.4 (2) (1/25) (1/Π) (25/4)

h  =  2.2/Π

h  =  0.7 m

Problem 4 :

A cylindrical bucket of height 32 cm and radius 18 cm is filled with sand. The bucket is emptied on the ground and a conical heap and sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.

Solution :

Volume of sand in the cylindrical bucket  =  Volume of sand of conical heap

Let r₁, h₁ be the radius and height of cylindrical tank

Let r₂, h₂ be the radius and height of conical tank

Π r₁²h₁  =  (1/3)Π r₂²h₂

r₁  =  18 cm,  h₁  =  32 cm and h₂  =  24 cm

18²(32)  =  (1/3) r₂²(24)

18²(32)  =  8 r₂²

r₂² =  (18⋅18⋅32)/8

r₂  =  18(2)

r₂  =  36 cm

So, the radius of the conical heap is 36 cm.

Problem 5 :

A solid toy is in the form of a right circular cylinder with a hemispherical shape at one end and a cone at the other end. Their common diameter is 4.2 cm and the height of the cylindrical and conical portions are 12 cm and 7 cm respectively. Find the volume of the solid toy.

Solution :

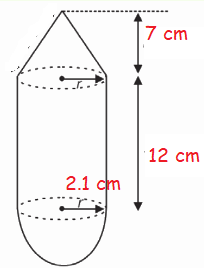
Volume of toy = Volume of hemisphere + volume of cylinder + volume of cone

= (2/3)Π r³ + Π r² h + (1/3)  Π r² h

= Π r² [(2/3)r + h + (1/3)h]

= Π (2.1)² [(2/3)2.1 + 12 + (1/3)7]

= Π (4.41) [2(0.7) + 12 + 2.3]

= 3.41(4.41) [1.4 + 12 + 2.3]

= 15.04 [15.7]

= 236.13 cm³

Problem 6 :

The radii of the internal and external surfaces of a metallic spherical shell are 3 cm and 5 cm respectively. It is melted and recast into a solid right circular cylinder of height 10 2/3. Find the radius of the base of the cylinder.

Solution :

From the given information, we know that it must be a hollow sphere.

Let external radius as R and internal radius be r.

Volume of hollow sphere = (4/3)Π (R³ - r³)

height of cylinder = 10  2/3

= 32/3

Volume of cylinder = Π r² h

(4/3) x Π(5³ - 3³) = Πr² x 32/3

1.33 x Π(125 - 27) = 10.6Πr²

1.33 x 98 = 10.6r²

r² = (1.33 x 98)/10.6

r² = 12.29

r = 3.5

So, the base radius is 3.5 cm.

Problem 7 :

Lead spheres of diameter 6 cm are dropped into beaker containing some water and are fully submerged. The diameter of the beaker is 18 cm. Find how many lead spheres have been dropped in it if the water rises by 40 cm?

Solution :

Let n be the number of lead spheres to be submerged.

Radius of the sphere = 3 cm

Radius of cylinder = 18/2 ==> 9 cm

Volume of sphere dropped = quantity of water raises

n (4/3) x Πr³ =  Π r² h

n (4/3) x 3³ =  9² (40)

n = (81 x 40 x 3) / (27 x 4)

n = 90

So, 90 spheres to be dropped.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.