VOLUME AND SURFACE AREA OF COMBINED SHAPES QUESTIONS

Question 1 :

A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter is 14 cm and the height of the vessel is 13 cm. Find the capacity of the vessel.

Solution :

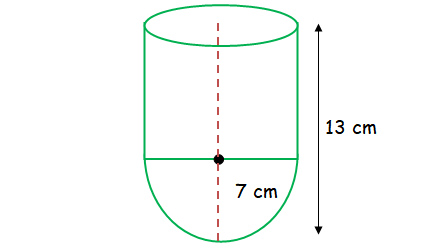
Height of vessel  =  13 cm

radius of hemisphere + height of cylinder  =  13

7 + h  =  13

h  =  13 - 7  =  6 cm

Volume of vessel 

  =  volume of hemisphere + volume of cylinder

  =  (2/3)πr³ + πr² h

  =  πr²[(2/3) r + h]

  =  (22/7) 7²[(2/3) 7 + 6]

  =  (22/7) 49 (32/3)

  =  1642.67 cm³

Question 2 :

Nathan, an engineering student was asked to make a model shaped like a cylinder with two cones attached at its two ends. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of the model that Nathan made.

Solution :

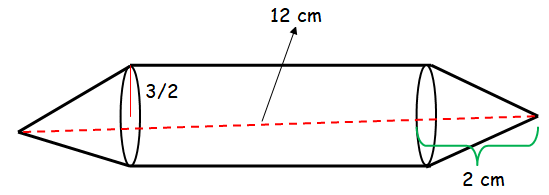
Volume of model  =  2 volume of cones + volume of cylinder

  =  2 (1/3)πr²h + πr²h

Height of the model  =  12 

2(height of cone) + height of cylinder  =  12

2(2) + h  =  12

height of cylinder  =  8 cm

  =  πr²[(2/3) 2 + 8]

  =  (22/7) (3/2)²[(4/3) + 8]

=  (22/7) (9/4) (28/3)

Volume of model  =  66 cm³

Question 3 :

From a solid cylinder whose height is 2.4 cm and the diameter 1.4 cm, a cone of the same height and same diameter is carved out. Find the volume of the remaining solid to the nearest cm³ .

Solution :

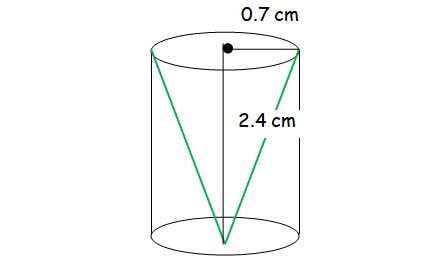
Volume of remaining solid  =  Volume of cylinder - Volume of cone

  =  πr²h - (1/3) πr²h

  =  πr²h[1 - (1/3)]

  =  (22/7)(0.7)²(2.4) (2/3)

  =  (22/7)(0.7)²(2.4) (2/3)

  =  2.46 cm³

Question 4 :

A solid consisting of a right circular cone of height 12 cm and radius 6 cm standing on a hemisphere of radius 6 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of the water displaced out of the cylinder, if the radius of the cylinder is 6 cm and height is 18 cm.

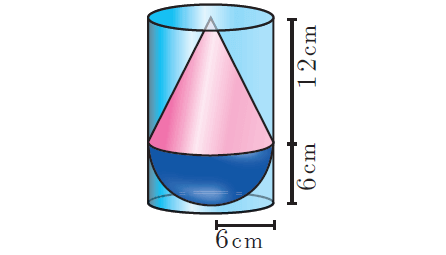
Solution :

Volume of water displaced 

  =  Volume of water in the cylinder - (Volume of cone + Volume hemisphere)

  =   πr²h - [(1/3) πr²h +  (2/3)πr³]

  =   πr²h - (1/3) πr²h - (2/3)πr³

  =   πr² (h -(1/3)h - (2/3)r)

  =   (22/7)6² (18 -(1/3)(12) - (2/3)(6))

  =   (22/7) 36 (18 - 4 - 4)

  =   (22/7) 36 (10)

  =  1131.42 cm³

Question 5 :

A roof is shaped like a square pyramid. One bundle of shingles covers 25 square feet. How many bundles should you buy to cover the roof ?

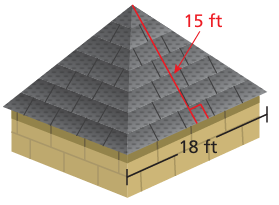
Solution :

Surface area of the roof = 4 x area of triangle

= 4 x (1/2) x base x height

base = 18 ft and height = 15 ft

= 2 x 18 x 15

= 540 square feet

One bundle can cover 25 square feet

Number of bundles needed = 540/25

= 21.6

Approximately 22 bundles is needed.

Question 6 :

You are making an umbrella that is shaped like a regular octagonal pyramid.

a. Estimate the amount of fabric that you need to make the umbrella.

b. The fabric comes in rolls that are 72 inches wide. You don’t want to cut the fabric “on the bias.” Find out what this means. Then draw a diagram of how you can cut the fabric most effi ciently.

c. How much fabric is wasted?

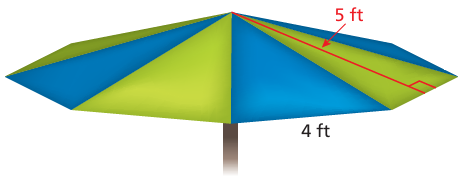
Solution :

a) Amount of fabric needed to make umbrella

= 8 x area of triangle

= 8 x (1/2) x base x height

base of triangle = 4 ft

height of triangle = 5 ft

1 feet = 12 inches

base in inches = 4 x 12 ==> 48 inches

height in inches = 5 x 12 ==> 60 inches

Amount of fabric is needed = 4 x 48 x 60

= 11520 square inches.

b)  The most efficient way,

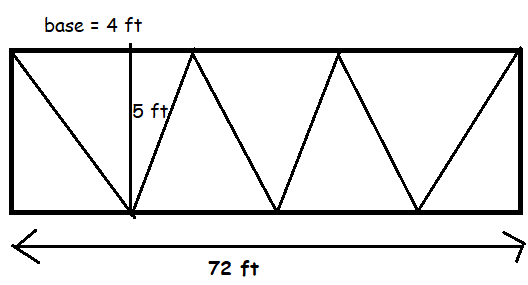
Determine the dimensions of the fabric needed. The fabric roll is 72 inches wide. To minimize waste, we need to find the length needed. The area is 11520 square inches, so the length is

= 11520/72

= 160 inches

Calculate the total area of the fabric used. The total area of the fabric used is

160 x 72 = 11520

Calculate the wasted fabric :

There is no wasted fabric in this scenario as the entire piece of fabric is used.

Question 7 :

Find the surface area of the cylinder. Round your answer to the nearest tenth.

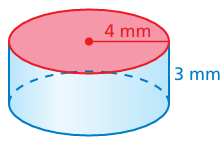
Solution :

S = 2π r ² + 2π rh

= 2π (4)² + 2π (4)(3)

= 32π + 24π 4 mm 3 mm

= 56π

≈ 175.8

The surface area is about 175.8 square millimeters.

Question 8 :

Two liters of water are poured into an empty vase shaped like an octagonal prism. The base area is 100 square centimeters. What is the height of the water? (1 L = 1000 cm³)

Solution :

Volume of octogonal prism = base area x height

2 liters of water = 2 x 1000

= 2000 cm³

Let h be the height of octogonal prism.

2000 = 100 x h

h = 2000/100

h = 20 cm

So, the required height is 20 cm.

Question 9 :

What is the approximate surface area of a cylinder with a radius of 3 inches and a height of 10 inches?

a) 30 in²    b) 87 in²   c)  217 in²  d) 245 in²

Solution :

Radius = 3 inches and height = 10 inches

Total surface area of cylinder = 2π r(h + r)

= 2 x 3.14 x 3 x (10 + 3)

= 244.92 square inches

Approximately 245 square inches. Option d is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.