USING TABLES TO COMPARE RATIOS WORKSHEET

Question 1 :

Find which ratio is greater :

2 1/3 : 3 1/3 and 3.6 : 4.8

Solution :

If we want to compare two ratios using table, both the terms of the ratio must be integers. 

Let us convert the terms of the first ratio into integers. 

2 1/3  :  3  1/3  =  (7/3) : (10/3)

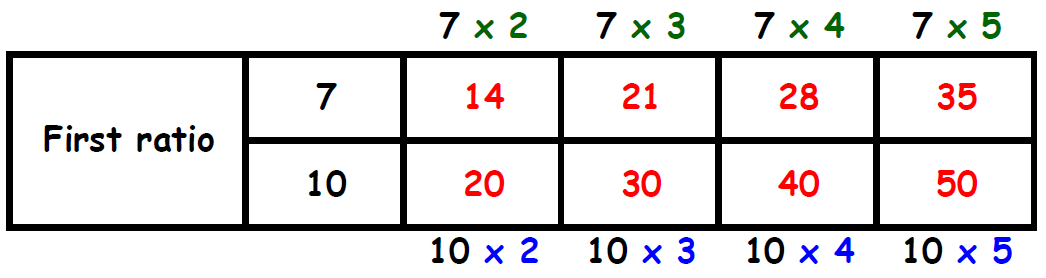
2 1/3  :  3  1/3  =  7 : 10 ------> multiplied by 3 

Let us write equivalent ratios to the ratio 7 : 10

Let us convert the terms of the second ratio into integers. 

3.6 : 4.8  =  36 : 48 ------> multiplied by 10 

3.6 : 4.8  =  3 : 4 ------> divided by 12 

Let us write equivalent ratios to the ratio 3 : 4

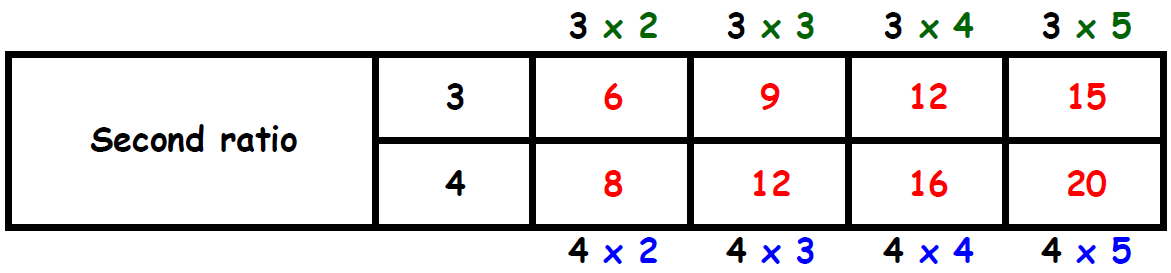
Find two columns, one in each table, in which the the second term is same. Circle those two columns.

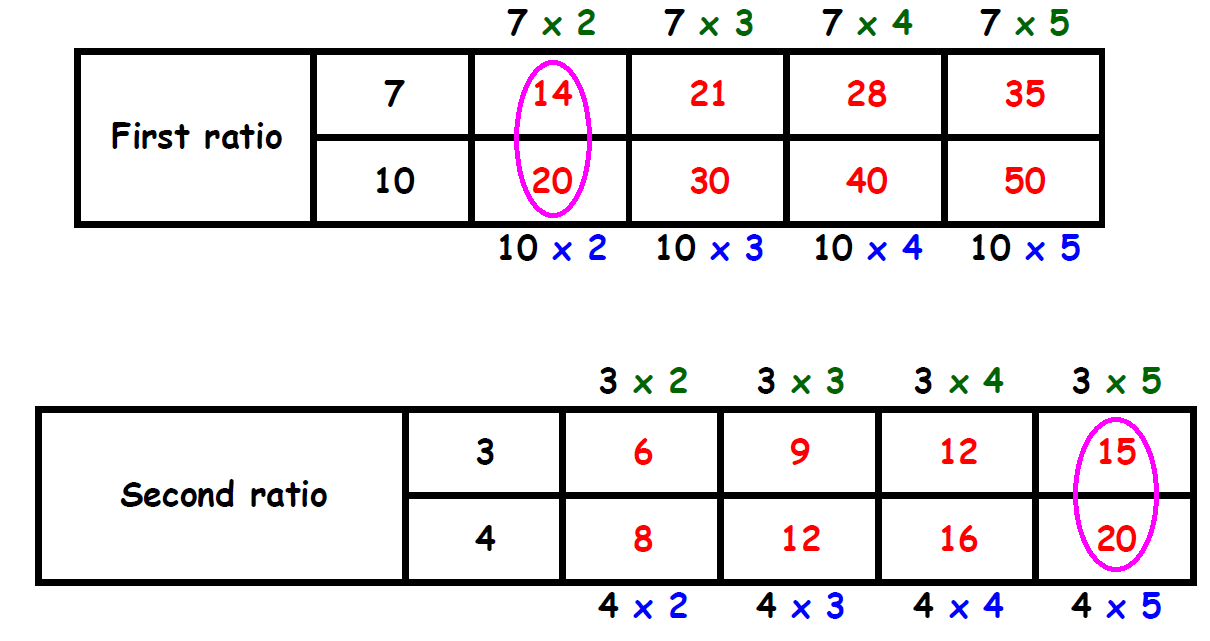
From the circled columns, we get two ratios. 

They are, 

14 : 20 and 15 : 20

In these two ratios, the second term is same. 

So, we have to compare the first terms 14 and 15.

The first term in the second ratio (15) is more than the first term in the first ratio (14).  

Therefore, the second ratio is greater than the first ratio. 

That is, 3.6 : 4.8 is greater than 2 1/3 : 3 1/3.  

Question 2 :

Anna’s recipe for lemonade calls for 2 cups of lemonade concentrate and 3 cups of water. Bailey’s recipe calls for 3 cups of lemonade concentrate and 5 cups of water. Whose recipe makes stronger lemonade? How do you know ?

Solution :

Anna’s recipe :

2 cups of lemonade and 3 cups of water.

So, the ratio is 2 : 3.

Let us write equivalent ratios to the ratio 2 : 3.

Bailey’s recipe :

3 cups of lemonade and 5 cups of water.

So, the ratio is 3 : 5.

Let us write equivalent ratios to the ratio 3 : 5.

Find two columns, one in each table, in which the amount of water is the same. Circle those two columns.

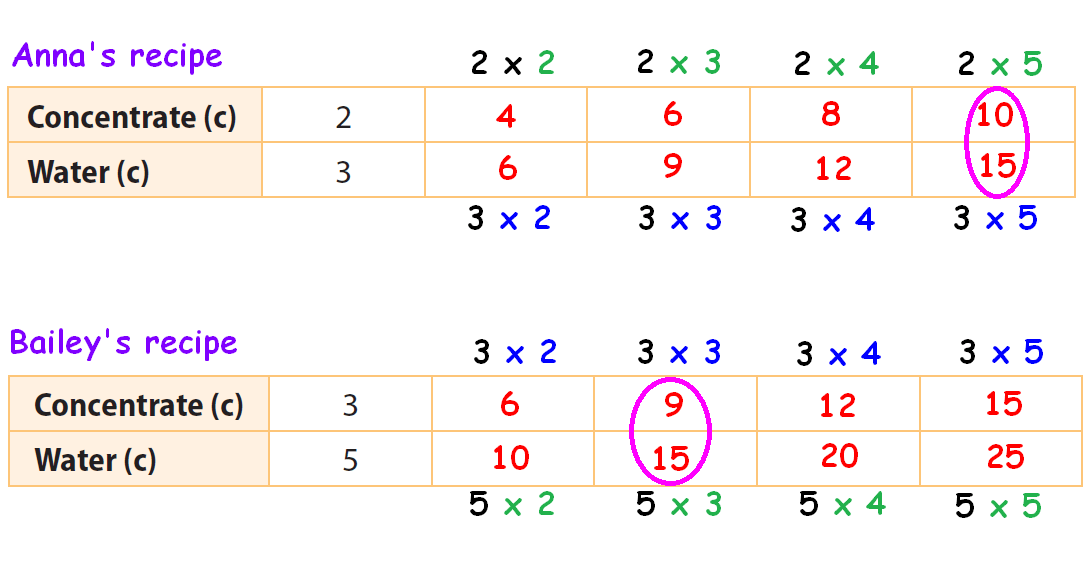
From the circled columns, we get two ratios. 

They are, 

10 : 15 and 9 : 15

In these two ratios, the second quantity (water) is same. 

So, we have to compare the first quantity (Lemonade).

The first quantity (10) in the first ratio is more than the first quantity (9) in the second ratio. 

When the quantity of water is same (15) in both recipes, Anna's recipe has more quantity of lemonade concentrate.

Therefore, Anna's recipe has stronger lemonade. 

Question 3 :

The table shows the numbers of stamps in a new stamp collection. Use ratio language to compare the number of celebrity stamps to the total number of stamps.

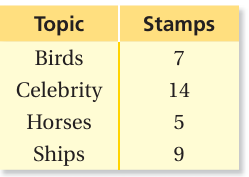
Solution :

Total number of stamps = 7 + 14 + 5 + 9

= 35

Total number of celebrity stamps = 14

Ratio between celebrity stamps to total number of stamps

= 14 : 35

= 14/35

= 2/5

= 2 : 5

Question 4 :

The nutrition facts label on a box of crackers shows that there are 240 milligrams of sodium in every 36 crackers.

a. You eat 15 crackers. How much sodium do you consume?

b. You eat 21 crackers. How much sodium do you consume?

Solution :

Quantity of sodium = 240 mg

Number of crackers consuming = 36

a) 

Let x be the quantity of sodium consuming when 15 crackers are eaten.

36 : 240 = 15 : x

36/240 = 15/x

36x = 15(240)

x = 15(240)/36

x = 100

b)

Let x be the quantity of sodium consuming when 21 crackers are eaten.

36 : 240 = 21 : x

36/240 = 21/x

36x = 21(240)

x = 21(240)/36

x = 5040/36

x = 140

Question 5 :

The nutrition facts label on a container of dry roasted cashews indicates there are 161 calories in 28 grams. You eat 9 cashews totaling 12 grams. How many calories do you consume?

Solution :

Weight of cashews = 28 grams

Number of calories = 161

Let x be the number of calories consuming when 12 grams of cashews.

28 : 161 = 12 : x

28/161 = 12/x

28x = 12(161)

x = 12(161) / 28

x = 69

Question 6 :

Seven out of every 8 students surveyed owns a bike. The difference between the number of students who own a bike and those who do not is 72. How many students were surveyed?

Solution :

Number of students owns a bike = 7

Total number of students = 8

Students who donot own a bike = 1

Ratio of the students own a bike : donot own a bike = 7 : 1

7x - 1x = 72

6x = 72

x = 72/6

x = 12

Number of students who is surveyed = 7x + 1x

8x

= 8(12)

= 96 students

Question 7 :

A piece of space junk travels 5 miles in 8 seconds. How far does it travel per second?

Solution :

Distance traveled = 5 miles

Time taken = 8 seconds

Distance traveled per second = 5/8

= 0.625 mile per second

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.