USING SIMILAR TRIANGLES TO EXPLAIN SLOPE

In similar triangles, corresponding angles are congruent and corresponding sides are proportional. 

Similar triangles can be used to explain slope. For example, we can use similar triangles to show that the slope of a line is constant.

Step 1 :

Draw a line ℓ that is not a horizontal line. Label four points on the line as D, F, A, and C.

Step 2 :

Draw the rise and run for the slope between points D and F. Label the intersection as point E. Draw the rise and run for the slope between points A and C. Label the intersection as point B.

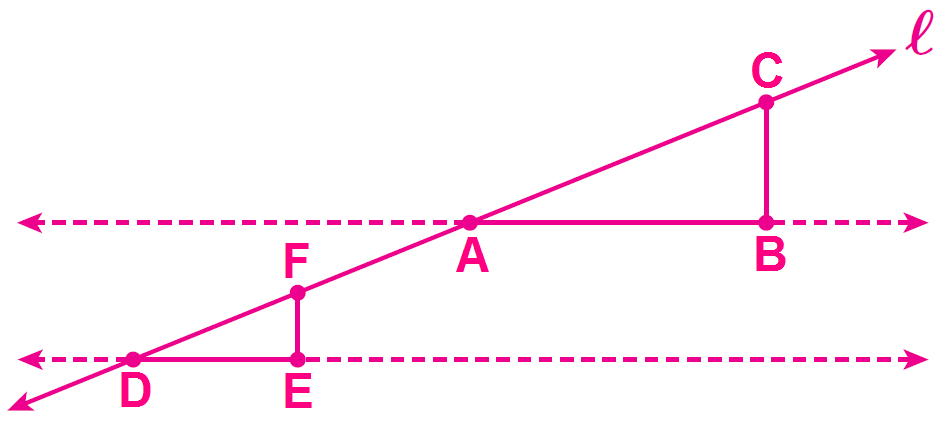
Aim :

We need to show that the slope between the points D and F is the same as the slope between the points A and C.

Step 3 :

Write expressions for the slope between D and F and between A and B. 

Slope between D and F :  FE / DE

Slope between A and B :  CB / AB

Step 4 :

Extend DE and AB across our drawing. DE and AB are both horizontal lines, so they are parallel.

Line l is a transversal that intersects parallel lines.  

Step 5 :

Because DE and AB are parallel lines and ℓ is a transversal that intersects DE and AB, 

m∠FDE and m∠CAB are corresponding angles and they are congruent. 

m∠FED and m∠CBA are right angles and they are congruent. 

Step 6 :

By Angle–Angle Similarity, triangle ABE and triangle CDF are similar triangles. 

Step 7 :

Because triangle ABE and CDF are similar, the lengths of corresponding sides of similar triangles are proportional.

FE / CB  =  DE / AB

Step 8 :

Recall that you can also write the proportion so that the ratios compare parts of the same triangle :

FE / DE  =  CB / AB

Step 9 :

The proportion we wrote in step 8 shows that the ratios we wrote in step 3 are equal. So, the slope of line ℓ is constant.

Reflect

Suppose that we label two other points on line ℓ as P and Q. Would the slope between these two points be different than the slope we found in the above activity ? Explain.

No

The slope of the line is constant, so the slope between the points P and Q would be the same. Moreover, not only the two points P and Q, between any two points on ℓ, the slope would be same. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.