USING EQUATIONS TO SOLVE PROBLEMS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To solve real world problems, we can use the relationship between the quantities and form equations which represent the situation given in the problem.
Then, we can use these equations to solve the problems.
Example 1 :
Juanita is scrapbooking. She usually completes about 9 pages per hour. One night last week she completed pages 23 through 47 in 2.5 hours. Did she work at her average rate ?
Solution :
Analyze Information :
Identify the important information.
• Worked for 2.5 hours
• Starting page: 23
• Ending page: 47
• Scrapbooking rate: 9 pages per hour
Formulate a Plan :
• Solve an equation to find the number of pages Juanita can expect to complete.
• Compare the number of pages Juanita can expect to complete with the number of pages she actually completed.
Solve :
Let n represent the number of pages Juanita can expect to complete in 2.5 hours if she works at her average rate of 9 pages per hour.
Write an equation.
n/2.5 = 9
Since we are trying to solve for "n", we have to get rid of 2.5 which divides n in the above equation.
To get rid of 2.5 in the above equation, we have to multiply by 2.5 on both sides.
2.5 x (n/2.5) = 2.5 x 9
n = 22.5
Juanita can expect to complete 22.5 pages in 2.5 hours.
Juanita completed pages 23 through 47, a total of 25 pages.
Because 25 > 22.5, she worked faster than her expected rate.
Justify and Evaluate :
We used an equation to find the number of pages Juanita could expect to complete in 2.5 hours if she worked at her average rate.
We found that she could complete 22.5 pages.
Since 22.5 pages is less than the 25 pages Juanita completed, she worked faster than her average rate.
The answer makes sense, because Juanita completed 25 pages in 2.5 hours, which is equivalent to a rate of 10 pages in 1 hour.
Since 10 > 9, we know that she worked faster than her average rate.
Example 2 :
Tion divides his baseball cards equally among himself, his brother, and 3 friends. He has 9 cards left. How many does he give away ? Write and solve an equation to solve the problem. Tell what the variable represents.
Solution :
Analyze Information :
Identify the important information.
• Baseballs cards are equally divided among five people. (Tion, his brother and 3 of his friends)
• When cards are divided equally among five people, Tion has 9 cards left. So each one gets 9 cards.
Formulate a Plan :
• Solve an equation to find the number of cards that Tion had initially.
• Subtract 9 from the cards that Tion had initially to find the number of cards he gave away.
Solve :
Let n represent the number of cards that Tion had initially.
Write an equation.
n/5 = 9
Since we are trying to solve for "n", we have to get rid of 5 which divides n in the above equation.
To get rid of 5 in the above equation, we have to multiply by 5 on both sides.
5 x (n/5) = 5 x 9
n = 45
Therefore, Tion had 45 baseball cards initially.
Justify and Evaluate :
We used an equation to find the number of baseball cards that Tion had initially.
We found that the number of baseball cards that Tion had initially is 45
The answer makes sense, because when we divide 45 by 5, we get 9 that Tion has left.
After dividing 45 cards equally among five people including himself, Tion has left with 9 cards.
Then the number of cards he gave away is
= 45 - 9
= 36
The variable we have taken to solve this problem is "n". And this variable "n" represents the number of baseball cards that Tion had initially.
Example 3 :
A discounted amusement park ticket costs $12.95 less than the original price p. Write and solve an equation to find the original price.

Solution :
Original price = pCost of discounted ticket = p - 12.50
From the picture, we know that discounted price = $44
p - 12.50 = 44
p = 44 + 12.50
p = 56.50
So, the originla price of the ticket is $56.50.
Example 4 :
You and a friend are playing a board game. Your final score x is 12 points less than your friend’s final score. Write and solve an equation to find your final score.
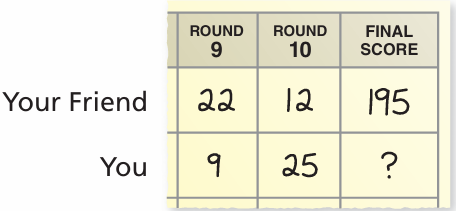
Solution :
Your final score :
x = your friend's score - 12
x = 195 - 12
x = 183
So, your final score will be 183.
Example 5 :
A baker orders 162 eggs. Each carton contains 18 eggs. Write the equation to find the number x of cartons? Explain your reasoning and solve the equation.
Solution :
Number of eggs = 162
Number of eggs in each carton = 18
Number of cartons = x
Number of cartons
= Total number of eggs / number of eggs in each carton
= 162/18
= 9
So, the required number of carons is 9.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

