USING DISTRIBUTIVE PROPERTY INVOLVING RADICALS WORKSHEET

Expand and simplify 

Problem 1  :

√2 (√5+√2)

(A)  √5+2     (B)  √10+2     (C)  √2+2     (D)  √5

Problem 2  :

√3 (1-√3)

(A)  √3-3     (B)  √3+1     (C)  1-√3     (D)  √3

Problem 3  :

√11 (2√11-1)

(A)  √11-2     (B)  22-√11     (C)  22     (D)  √11

Problem 4  :

2√3 (√3-√5)

(A)  √3+√5     (B)  √5     (C)  2√3     (D)  6-2√15

Problem 5  :

(1+√2) (2+√2)

(A)  2√2     (B)  4+3√2     (C)  6     (D)  √2

Problem 6  :

(√3+2) (√3-1)

(A)  1+√3     (B)  1     (C)  √3     (D)  2

Problem 7  :

(√5+2) (√5-3)

(A)  √5     (B)  3     (C)  -1-√5     (D)  1

Problem 8  :

(2√2+√3) (2√2-√3)

(A)  5     (B)  8     (C)  11     (D)  3

Problem 9  :

(2+√3) (2+√3)

(A)  2     (B)  √3     (C)  7+4√3     (D)  4 

Problem 10  :

(4-√2) (3+√2)

(A)  √2     (B)  10+√2     (C)  7     (D)  10

Problem 11  :

(√7-√3) (√7+√3)

(A)  3     (B)  4     (C)  7     (D)  10

Problem 12  :

(4-√2) (3-√2)

(A)  7√2     (B)  √2     (C)  14-7√2     (D)  3

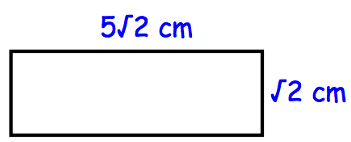
Problem 13 :

Shown below is a rectangle

Problem 14 :

Expand and simplify

(√3 + √5)²

Problem 15 :

Expand and simplify

√3(√27 - √3)

Problem 16 :

Given that a = √2, b = √15 and c = √30

work out the value of

b/ac

Write your answer in simplest form.

Problem 17 :

Given that a = √3 and b = √48

a)  work out the value of a²

b)  Show that (a+b)² = 75

Problem 18 :

Expand and simplify (3 + √8)(4 + √2) Give your answer in the form a + b √2 where a and b are integers

Problem 19 :

The midpoints of the sides of a square of side 10 cm are joined to form another square. This process is then repeated to create the shaded square.

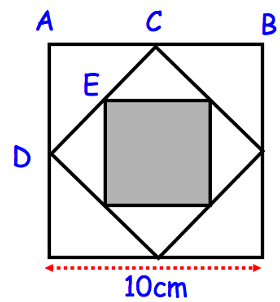
Find the area of the shaded square.

Problem 20 :

Given that (10 - √32)/√2 = a + b√2

Write a and b as integers, find the values of a and b.

1.Solution  :

Given, √2 (√5+√2)

By distribution, we get

√2 (√5+√2)  =  √2×√5 + √2×√2

=  √10+2

So, the answer is √10+2.

2.Solution  :

Given, √3 (1-√3)

By distribution, we get

√3 (1-√3)  =  √3×1 - √3×√3

=  √3-3

3.Solution  :

Given, √11 (2√11-1)

By distribution, we get

√11 (2√11-1)  =  √11×2√11 - √11×1

=  2×11 - √11

=  22-√11

4.Solution  :

Given, 2√3 (√3-√5)

By distribution, we get

2√3 (√3-√5)  =  (2√3×√3)-(2√3×√5)

=  (2x3) - 2√15

=  6-2√15

5.Solution  :

Given, (1+√2) (2+√2)

By distribution, we get

(1+√2) (2+√2)  =  2+√2+2√2+2

=  4+3√2

6.Solution  :

Given, (√3+2) (√3-1)

By distribution, we get

(√3+2) (√3-1)  =  (√3×√3)-(√3×1)+(2×√3)-(2×1)

=  3-√3+2√3-2

=  1+√3

7.Solution  :

Given, (√5+2) (√5-3)

By distribution, we get

(√5+2) (√5-3)  =  (√5×√5)-(√5×3)+(2×√5)-(2×3)

=  5-3√5+2√5-6

=  -1-√5

8.Solution  :

Given, (2√2+√3) (2√2-√3)

By algebraic identity, we get

(2√2+√3) (2√2-√3)  =  (2√2)²-(√3)²

=  4×2 - 3

=  5

9.Solution  :

Given, (2+√3) (2+√3)

By distribution, we get

(2+√3) (2+√3)  =  2×2+(2×√3)+(√3×2)+(√3×√3)

=  4+2√3+2√3+3

=  7+4√3

10.Solution  :

Given, (4-√2) (3+√2)

By distribution, we get

(4-√2) (3+√2)  =  (4×3)+(4×√2)-(√2×3)-(√2×√2)

=  12+4√2-3√2-2

=  10+√2

11.Solution  :

Given, (√7-√3) (√7+√3)

By using algebraic identity

(a+b)(a-b)  =  a²-b²

(√7-√3) (√7+√3)  =  (√7)²-( √3 )²

=  7-3

=  4

12.Solution :

Given, (4-√2) (3-√2)

By distribution, we get

(4-√2) (3-√2)  =  4×3 - (4×√2) - (√2×3) + (√2×√2)

=  12-4√2-3√2+2

=  14-7√2

13.Solution :

a) Perimeter of the rectangle = 2(length + width)

Length of the rectangle = 5√2

width of the rectangle = √2

= 2(5√2 + √2)

= 2(6√2)

= 12√2 cm

b) Area of the rectangle = length x width

= 5√2 (√2)

= 5(2)

= 10 cm²

14. Solution :

(√3 + √5)²

Using the formula for (a + b)² = a² + 2ab+ b²

Here a = √3 and b = √5

Expanding this using the formula above,

(√3 + √5)² = (√3)² + 2(√3)(√5) + (√5)²

= 3 + 2√15 + 5

= 8 + 2√15

15. Solution :

= √3(√27 - √3)

By distributing √3, we get

= √3(√27) - √3(√3)

= √(3 x 27) - 3

decomposing 27, we get

= √(3 x 3 x 3 x 3) - 3

= 9 - 3

= 6

So, the answer is 6.

16. Solution :

Given that, a = √2, b = √15 and c = √30

b/ac

Applying the given values, we get

= √15 / √2 √30

= √15 / √(2x30)

= √15 / √(2x2x3x5)

= √15 / 2√15

= 1/2

17. Solution :

Given that a = √3 and b = √48

a)  a² = √3²

 = 3

b)  (a+b)² = (√3 + √48) ²

= (√3 + √(4 x 4 x 3))²

= (√3 + 4√3)²

Before expanding this using algebraic identity, we know that both are like terms. So, we can combine.

= (5√3)²

= 25(3)

= 75

18. Solution :

(3 + √8)(4 + √2)

Using distributive property, we get

(3 + √8)(4 + √2) = 12 + 3√2 + 4√8 + √2(√8)

= 12 + 3√2 + 4√(2x2x2) + √(2x8)

= 12 + 3√2 + (4x2)√2 + √16

= 12 + 3√2 + 8√2 + 4

= 16 + 11√2 

By comparing this with a + b√2, we get

a = 16 and b = 11

19. Solution :

Length of the square = 10 cm

Finding the measure of DC :

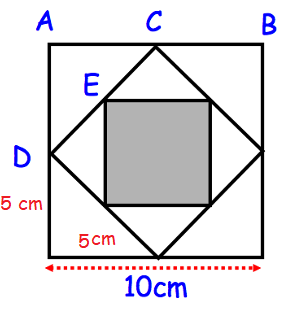
DC² = 5² + 5²

DC = √(25+25)

= √50

= √(5 x 5 x 2)

= 5√2

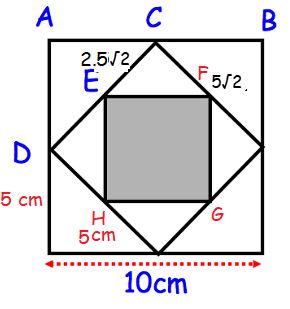
Area of shaded square

= Area of square EFGH - 4(Area of triangle CEF)

= (5√2)² - 4(1/2) x 2.5√2 x 2.5√2

= 25(2) - 2 x 6.25(2)

= 50 - 25

= 25 cm²

20. Solution :

Given that (10 - √32)/√2 = a + b√2

Multiplying both numerator and denominator by √2.

= [(10 - √32)/√2] [√2/√2]

= √2(10-√32)/2

√32 = √(2 x 2 x 2 x 2 x 2)

= 4√2

= √2(10-4√2)/2

= 2√2(5-2√2)

= 10√2 - 4√2√2

= 10 √2 - 8

= -8 + 10√2

Comparing with a + b√2

a = -8 and b = 10

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.