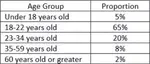
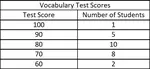
UNIT RATES WITH FRACTIONS

We can use unit rates to simplify rates and ratios that appear complicated, such as those containing fractions in both the numerator and denominator.

Example :

Two pools are leaking. After 15 minutes, pool A has leaked 2/3 gallon. After 20 minutes, pool B has leaked 3/4 gallon. Which pool is leaking faster ?

To find which pool is leaking faster,  we have to find leak per hour for each pool.  

Compare the unit rates.

2.67 > 2.25

So, Pool A is leaking greater

Solved Problems

Problem 1 :

Which is best,

10 pencils cost $4

or 

6 pencils cost $2.70?

Solution :

To compare the given measures, convert them in to unit rates. 

We get the lowest price per pencil $0.40 in "10 pencils cost $4"

So, "10 pencils cost $4" is the best deal.

Problem 2 :

Which is best,

2 liters of milk at $3.80

or 

1.5 liters of milk at $2.70?

Solution :

To compare the given measures, convert them in to unit rates. 

From the above unit rates, we get the lower price per liter of milk $1.8 in "2 liters cost $2.70"

So, "2 liters cost $2.70" is the best deal.

Problem 3 :

Who is better in earning,

David earns $57.60 in 8 hours

or 

John earns $90 in 12 hours?

Solution :

To compare the given measures, convert them in to unit rates. 

From the above unit rates, John earns more than David per hour. 

So, John is earning better.

Problem 4 :

Who is driving faster,

Alex covers 120 miles in 3 hours

or 

Jose covers 84 miles in 2 hours?

Solution :

To compare the given measures, convert them in to unit rates. 

From the above unit rates, Jose covers more miles than David per hour. 

So, Jose is driving faster.

Problem 5 :

Who is better,

Lily can prepare 10.4 gallons of juice in 4 days

or 

Rosy can prepare 7.5 gallons of juice in 3 days?

Solution :

To compare the given measures, convert them in to unit rates. 

From the above unit rates, Lily prepares more gallons than day. 

So, Lily is better.

Problem 6 :

Which is best,

500 grams cheese cost $ 3.25

or 

1.5 kilograms cheese cost $ 9.9

Solution :

To compare the given measures, convert them in to unit rates in price per kilogram. 

From the above unit rates, we get the lower price per kilogram $6.5 in "500 grams cheese cost $ 3.25"

So, "500 grams cheese cost $ 3.25" is the best deal.

Problem 7 :

Who is driving faster,

Lenin  covers 6 miles in 2 minutes

or 

Daniel covers 225 miles in 1.5 hours?

Solution :

To compare the given measures, convert them in to unit rates in distance per hour. 

From the above unit rates, Lenin covers more miles than Daniel per hour.

So, Lenin is driving faster.

Problem 8 :

Who is better in walking,

  Shanel walks 2/ 5 of a mile every 1/7 hour

or 

Declan walks 3/5 of a mile every 2/7 hour?

Solution :

To compare the given measures, convert them in to unit rates in miles per hour (speed).

Speed  =  Distance/Time 

From the above unit rates, Shanel walk more miles than Declan per hour.

So, Shanel is better in walking.

Problem 9 :

Who is better,

 Daniel answered 240 answers correctly out of 300 questions

or 

Deborah answered 328 questions correctly out of 400 questions?

Solution :

To compare the given measures, convert them in to percentages.

Percent :

= [no. of correct answers/To tal no. of questions] x 100%

From the above percentages, Deborah answered more questions correctly than Daniel per 100. 

Hence, Deborah is better.

Problem 10 :

Which is best,

Plan A : Income of $250 on $5000 investment

or

Plan B : Income of $280 on $7000 investment

Solution :

To compare the given measures, convert them in to percentages of income.

Percent of income :

= [Income/Investment] x 100% 

From the above percentages, plan A gives more income than plan B per $100 investment.  

So, plan A is better.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.