TRIGONOMETRY PRACTICE QUESTIONS FOR GRADE 10

(1)  Prove that 

Solution

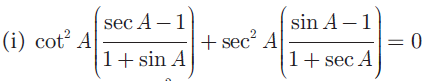
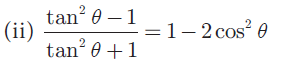
(2)  Prove that 

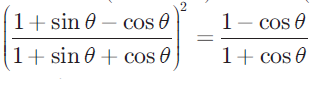
(3)  If x sin³ θ + y cos³ θ  = sin θ cos θ and x sin θ = y cos θ , then prove that x² + y² = 1.      Solution

(4)  If a cos θ - b sin θ  =  c, then prove that (a sin θ + b cos θ)  =  ± √(a² + b² - c²)      Solution

(5)  A bird is sitting on the top of a 80 m high tree. From a point on the ground, the angle of elevation of the bird is 45° . The bird flies away horizontally in such away that it remained at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30° . Determine the speed at which the bird flies.(√3 = 1.732)                 Solution

(6)  An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37° at a given point. After what period of time does the angle of elevation increase to 53° ? (tan 53° = 1.3270, tan 37° = 0.7536)          Solution

(7)  A bird is flying from A towards B at an angle of 35° , a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away.

(i) How far is B to the North of A?

(ii) How far is B to the West of A?

(iii) How far is C to the North of B?

(iv) How far is C to the East of B?

(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)                Solution

(8)  Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is 200[(√3  + 1)/√3] metres, find the height of the lighthouse.         Solution

(9)  A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34° . Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)                Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.